题目内容
17.已知1<x<2,试化简$\frac{|x-2|}{x-2}$-$\frac{x-1}{|1-x|}$+$\frac{|x|}{x}$.分析 根据绝对值的定义即可得到结论.
解答 解:∵1<x<2,
∴1-x<0,x-2<0,
∴$\frac{|x-2|}{x-2}$-$\frac{x-1}{|1-x|}$+$\frac{|x|}{x}$=$\frac{2-x}{x-2}+\frac{x-1}{x-1}+\frac{x}{x}$=-1+1+1=1.
点评 本题考查了绝对值的定义,分式的化简,熟记绝对值的 定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.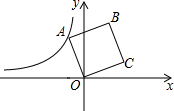 如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
 如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )| A. | -2 | B. | -4 | C. | -$\frac{15}{4}$ | D. | $\frac{15}{4}$ |
6. 第17届运动会于2014年09月19日~2014年10月04日在韩国仁川举行,图1是本届亚运会的吉祥物,象征着希望、速度和乐观向上的体育精神,某商店将吉祥物按成本价提高40%后标价,又以9折(即标价的90%)优惠卖出,结果每个吉祥物的售价为52元,设吉祥物的成本价为x元,可列方程为( )
第17届运动会于2014年09月19日~2014年10月04日在韩国仁川举行,图1是本届亚运会的吉祥物,象征着希望、速度和乐观向上的体育精神,某商店将吉祥物按成本价提高40%后标价,又以9折(即标价的90%)优惠卖出,结果每个吉祥物的售价为52元,设吉祥物的成本价为x元,可列方程为( )
 第17届运动会于2014年09月19日~2014年10月04日在韩国仁川举行,图1是本届亚运会的吉祥物,象征着希望、速度和乐观向上的体育精神,某商店将吉祥物按成本价提高40%后标价,又以9折(即标价的90%)优惠卖出,结果每个吉祥物的售价为52元,设吉祥物的成本价为x元,可列方程为( )
第17届运动会于2014年09月19日~2014年10月04日在韩国仁川举行,图1是本届亚运会的吉祥物,象征着希望、速度和乐观向上的体育精神,某商店将吉祥物按成本价提高40%后标价,又以9折(即标价的90%)优惠卖出,结果每个吉祥物的售价为52元,设吉祥物的成本价为x元,可列方程为( )| A. | (1+40%)x-52=90%x | B. | 40%x×90%-x=52 | C. | (1+40%)x×90%+x=52 | D. | (1+40%)x×90%=52 |
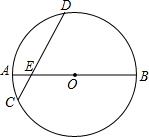 如图所示,已知⊙O的直径AB和弦CD相交于点E,AE=1cm,BE=5cm,∠BED=60°,求DE的长.
如图所示,已知⊙O的直径AB和弦CD相交于点E,AE=1cm,BE=5cm,∠BED=60°,求DE的长.