题目内容
若一个n边形的内角和为1440°，则其边数n的值是（ ）
| A、6 | B、8 | C、10 | D、12 |
考点：多边形内角与外角
专题：
分析：多边形的内角和可以表示成（n-2）•180°，列方程可求解．
解答：解：设所求多边形边数为n，
则（n-2）•180°=1440°，
解得n=10．
故选C．
则（n-2）•180°=1440°，
解得n=10．
故选C．
点评：本题考查根据多边形的内角和计算公式求多边形的边数，比较简单．
练习册系列答案
相关题目
将二次函数y=-x2-4x+2化为y=a（x+m）2+k的形式，则（ ）
| A、a=-1，m=-2，k=6 |
| B、a=-1，m=2，k=6 |
| C、a=1，m=-2，k=-6 |
| D、a=-1，m=2，k=-6 |
下列说法中，正确的是（ ）
| A、两个全等的图形一定成轴对称 |
| B、两个全等的图形一定是轴对称图形 |
| C、两个成轴对称的图形一定全等 |
| D、两个成轴对称的图形一定不全等 |
如图是小兵一天上学、放学时看到的一根电线杆的影子的俯视图，将它们按时间先后顺序进行排列，排列正确的是（ ）
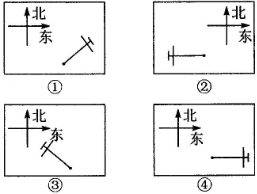
| A、①②③④ | B、②③④① |
| C、②③①④ | D、③①④② |
已知a-b=3，ab=10，那么a2+b2的值为（ ）
| A、27 | B、28 | C、29 | D、30 |
作图题：已知点A，B，C为三个村庄的位置（如图），三村联合打一口井，向三个村庄供水，使水井到三个村庄的距离相等，水井的位置应设在何处？请用尺规画出水井位置，不写作法，保留痕迹．