Question

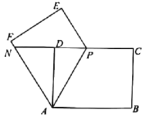
【题目】已知，四边形是正方形，点在边上，点在边的延长线上，且，连接．

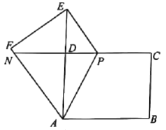
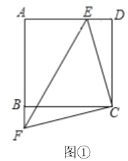
（1）如图①，连接．求证：是等腰直角三角形；

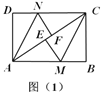
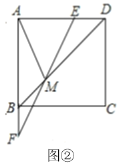
（2）如图②，与交于点，若正方形的边长为6，，求的长．

（3）点，点分别在边，边上，与交于点，且，若正方形的边长为6．求的长（直接写出结果即可）

Answer 1

【答案】（1）见解析；（2）；（3）3

【解析】

（1）证明△CDE≌△CBF即可得出结论；

（2）过作于，构建直角△AGM，证明△FGM∽△FAE，得FG＝2GM，设GM＝x，则FG＝2x，根据正方形的性质可得△BGM是等腰直角三角形，则可求出AG＝4，GM＝2，由勾股定理可得AM的长；

（3）过G作GP⊥CD于P，证明△GHP≌△CED，可得CE＝GH＝，在中利用勾股定理可求得DE的长．

解：（1）∵四边形是正方形，

∴，

∴，

在和中，，

∴，

∴，

∴，

∴是等腰直角三角形；

（2）如图，过作于，

∵，

∴，

∵，

∴，

∴，

∴，

∴，

设，则，

∵四边形是正方形，

∴，

∴是等腰直角三角形，

∴，

∴，

∴，

∴；

（3）如图，过作于，

由（1）知：，

∵，

∴，

∴，

∴，

∵，

∴，

∵，

∴，

∴，

∵，

在中，由勾股定理得：．