Question

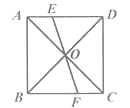
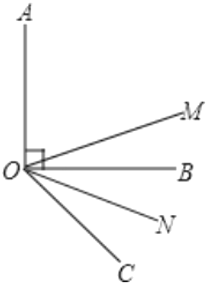
【题目】一扇窗户如图1所示，窗框和窗扇用“滑块铰链”连接．如图2是图1中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，支点4处装有滑块，滑块可以左右滑动，支点B，C,D在一条直线上，延长DE交MN于点F．已知AC=DE=20cm，AE=CD=10cm，BD=40cm．

（1）当∠CAB=35 时，求窗扇与窗框的夹角∠DFB的度数．

（2）当窗扇关闭时，图中点E，A,D，C,B都在滑轨MN上．求此时点A与点B之间的距离．

（3）在(2)的前提下，将窗户推开至四边形ACDE为矩形时，求点A处的滑块移动的距离．

Answer 1

【答案】（1）35°；（2）50，（3）

【解析】（1）根据两组对边分别相等的四边形是平行四边形，可证明四边形AEDC是平行四边形，再根据平行四边形的性质，证明DF∥AC，从而可求出结果；

（2）将图形抽象出来。先求出BC的长，再根据AB=AC+CB，就可求出答案；

（3）根据题意画出图形，利用勾股定理求出A1B的长，再利用A1A=AB-A1B，即可解答.

（1）解：∵AC=DE，AE=CD

∴四边形AEDC是平行四边形

∴DF∥AC

∴∠DFB=∠CAB=35°

（2）解：如图

∵BC=BD-CD=40-10=30

∴AB=AC+CB=20+30=50

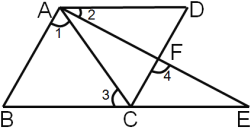
（3）解：如图，窗户户推开至四边形A1CDE为矩形时

在Rt△A1CB中，A1B=

∴点A处的滑块移动的距离A1A=AB-A1B=50-.