题目内容
如图，梯形ABCD中，AD∥BC，∠A=90°，E在AD上，且CE平分∠BCD，BE平分∠ABC，则下列关系式中成立的有（ ）①
| CD |
| AB |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
| A、2个 | B、3个 | C、4个 | D、5个 |
分析：根据角平分线的性质，推出角相等，再得出边相等，判断出①②正确，再利用三角形不相似，排除其它选项，最后得解．
解答：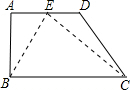
解：如图，∵BE平分∠ABC，
∴∠ABE=∠CBE．
∵AD∥BC，
∴∠AEB=∠EBC．
∴∠ABE=∠AEB，AB=AE．
同理ED=CD．
∴①
=
正确，②
=
正确；
由于△ABE与△CDE不相似，故③
=
不正确；
由于∠CED≠∠CBE=45°，
∴△CDE与△CEB不相似．
故④CE2=CD×BC不正确；
∵∠AEB=45°≠∠ECB，
∴△AEB与△EBC不相似．
故BE2=AE×BC不正确．
因此只有①②正确．
故选A．
解：如图，∵BE平分∠ABC，∴∠ABE=∠CBE．
∵AD∥BC，
∴∠AEB=∠EBC．
∴∠ABE=∠AEB，AB=AE．
同理ED=CD．
∴①
| CD |
| AB |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
由于△ABE与△CDE不相似，故③
| CE |
| DE |
| BE |
| AB |
由于∠CED≠∠CBE=45°，
∴△CDE与△CEB不相似．
故④CE2=CD×BC不正确；
∵∠AEB=45°≠∠ECB，
∴△AEB与△EBC不相似．
故BE2=AE×BC不正确．
因此只有①②正确．
故选A．
点评：本题利用了平行线的性质，角的平分线的性质，等边对等角，相似三角形的判定和性质求解．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
已知，如图，梯形ABCD中，AD∥BC，∠B=45°，∠C=120°，AB=8，则CD的长为（ ）A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
5、已知：如图，梯形ABCD中，AD∥BC，AB=DC，AC、BD相交于点O，那么，图中全等三角形共有
10、如图，梯形ABCD中，AD∥BC，BD为对角线，中位线EF交BD于O点，若FO-EO=3，则BC-AD等于（ ）
如图，梯形ABCD中，已知AD∥BC，∠A=90°，AB=7，AD=2，
如图，梯形ABCD中，AD∥BC，BC=5，AD=3，对角线AC⊥BD，且∠DBC=30°，求梯形ABCD的高．