题目内容
7.已知:在△ACB和△DCE中,CA=CB,CD=CE,点A、D、E在同一直线上,连接BE.(1)如图1,当∠ACB=∠DCE=60°时,
填空:①∠AEB的度数为60°;
②线段AD、BE之间的数量关系是AD=BE.
(2)如图2,当∠ACB=∠DCE=90°,试求∠AEB的度数,判断线段AD、BE之间的数量关系,并说明理由.
(3)若∠ACB=∠DCE=n°,则∠AEB的度数为n°.

分析 (1)根据等边三角形的判定和性质得出∠AEB的度数即可,先证出∠ACD=∠BCE,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(2)由(1)证得△ACD≌△BCE,得到∠ADC=∠BEC通过等量代换得到∠DCB=∠EBC,那么△ACD≌△BCE,根据全等三角形证出AD=BE;
(3)证明△ACD≌△BCE,得出∠ADC=∠BEC,由△DCE为等腰三角形,得到∠CDE=∠CED=90°-$\frac{1}{2}$n,因为点A,D,E在同一直线上,得到∠ADC=90°+$\frac{1}{2}$n,∠BEC=90°+$\frac{1}{2}$n,于是得到∠AEB=∠BEC-∠CED=n.
解答 (1)①∵在△ACB和△DCE中,CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴△ACB和△DCE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD=60°-∠CDB=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠ADC=∠BEC=120°,AD=BE,
∴∠AEB=∠BEC-∠CED=120°-60°=60°,
故答案为:①60;②AD=BE;
(2)∵∠ACB=∠DCE=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠ECB,
∵CA=CB,CD=CE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△CDA≌△CEB,
∴AD=BE;
由△CDA≌△CEB得∠CEB=∠CDA
∵CD=CE,∠DCE=90°,
∴△DCE是等腰直角三角形,
∴∠CDE=∠CED=45°,
∴∠CEB=∠CDA=135°,
∴∠AEB=90°;
(3)∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵△DCE为等腰三角形,
∴∠CDE=∠CED=90°-$\frac{1}{2}$n,
∵点A,D,E在同一直线上,
∴∠ADC=90°+$\frac{1}{2}$n,∠BEC=90°+$\frac{1}{2}$n,
∴∠AEB=∠BEC-∠CED=n,
故答案为:n.
点评 此题考查了全等三角形的判定与性质和等腰三角形的判定与性质以及等腰三角形的性质;证明三角形全等是解决问题的关键.

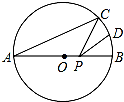 如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
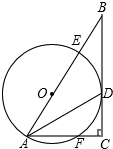 知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上.
知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上. 如图,∠B=30°,∠A′=60°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C的度数为90°.
如图,∠B=30°,∠A′=60°,△ABC与△A′B′C′关于直线l对称,则△ABC中的∠C的度数为90°. 如图,方格纸上画有两条线段,请再画1条线段,使图中的3条线段组成一个轴对称图形(找出符合条件的所有线段).
如图,方格纸上画有两条线段,请再画1条线段,使图中的3条线段组成一个轴对称图形(找出符合条件的所有线段).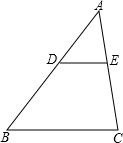 如图,△ABC中,D、E分别在AB、AC上,且DE∥BC,DE=2,BC=5,S△ABC=40,求S四边形BCED.
如图,△ABC中,D、E分别在AB、AC上,且DE∥BC,DE=2,BC=5,S△ABC=40,求S四边形BCED.