题目内容
如图,在△ABC中,∠ACB=80°,AD是BC边上的高,AE平分∠BAC, ∠BAE=30°
∠BAE=30°
(1)求∠ABC的度数;
(2)求∠DAE的度数.

【考点】三角形内角和定理;三角形的角平分线、中线和高;三角形的外角性质.
【分析】(1)首先根据AE平分∠BAC,∠BAE=30°,求出∠BAC的度数是多少,然后在△ABC中,根据三角形的内角和定理,求出∠ABC的度数是多少即可.
(2)首先根据三角形的外角的性质,求出∠AED的度数是多少;然后根据AD是BC边上的高,可得∠ADE=90°,据此求出∠DAE的度数是多少即可.
【解答】解:(1)∵AE平分∠BAC,∠BAE=30°,
∴∠BAC=2∠BAE=2×30°=60°,
∴∠ABC=180°﹣∠ACB﹣∠BAC=180°﹣80°﹣60°=40°.
(2)∵∠AED是△ABE的一个外角,
∴∠AED=∠ABC+∠BAE=40°+30°=70°,
∵AD是BC边上的高,
∴∠ADE=90°,
∴∠DAE=90°﹣70°=20°.
【点评】(1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360 °.②三角形的一个外角等于和它不相邻的两个内角的和.③三
°.②三角形的一个外角等于和它不相邻的两个内角的和.③三 角形的一个外角大于和它不相邻的任何一个内角.
角形的一个外角大于和它不相邻的任何一个内角.
(3)此题还考查了三角形的角平分线的性质和应用,要熟练掌握.

练习册系列答案
相关题目


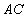 是底面圆的直径,高
是底面圆的直径,高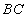 = 6cm,点
= 6cm,点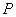 是母线
是母线 =
=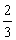
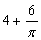 )cm B.5cm C.
)cm B.5cm C. cm D.7cm
cm D.7cm