题目内容
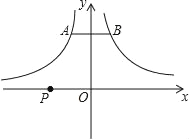
【题目】如图，点A（m，2），B（n，2）分别是反比例函数y＝﹣
，y＝
在x轴上方的图象上的点，点P是x轴上的动点，则PA+PB的最小值为_____．
【答案】5
【解析】
作A关于x轴的对称点C，连接BC，交x轴于P，则P即为使PA+PB有最小值的点，根据轴对称的性质求得C的坐标，然后求得BC即可．
∵点A（m，2），B（n，2）分别是反比例函数y＝﹣
，y＝
在x轴上方的图象上的点，
∴2＝﹣
，解得m＝﹣2，
2＝
，解得n＝1，
∴A（﹣2，2），B（1，2），
作A关于x轴的对称点C，连接BC，交x轴于P，则P即为使PA+PB有最小值的点，此时PA+PB＝BC；
∴C（﹣2，﹣2），
∴BC＝
＝5；
∴PA+PB的最小值为5；
故答案是：5．
练习册系列答案
阅读快车系列答案
相关题目
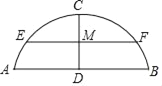
【题目】如图，在左边托盘A（固定）中放置一个生物，在右边托盘B（可左右移动）中放置一定重量的砝码，可使得仪器左右平衡，改变托盘B与支撑点M的跳高，记录相应的托盘B中的砝码质量，得到下表：
托盘B与点M的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y（g） | 30 | 20 | 15 | 12 | 10 |
（1）把上表中（x，y）的各级对应值作为点的坐标，在如图所示的平面直角坐标系中描出其余的点，并用一条光滑的曲线连接起来，观察所画的图象，猜想y与x的函数关系，求出该函数关系式.
（2）当托盘B向左移动（不能超过点M）时，应往托盘B中添加砝码还是减少砝码？为什么？
