��Ŀ����
18�����и�ʽ���������У���ȷ���ǣ�������| A�� | $\frac{3}{x}$��$\frac{x}{3}$=$\frac{9}{x}$ | B�� | ��$\frac{1}{x-3}-\frac{x+1}{{x}^{2}-1}$��•��x-3��=$\frac{2}{x-1}$ | ||
| C�� | ��$\frac{a}{a-2}-\frac{a}{a+2}$��•$\frac{4-{a}^{2}}{a}$=4 | D�� | ��$\frac{{b}^{2}}{a+b}-\frac{{a}^{2}}{a+b}$��•$\frac{ab}{a-b}$=ab |
���� ֱ�����÷�ʽ������㷨��ֱ��ʽ�ó��𰸣�
��� �⣺A��$\frac{3}{x}$��$\frac{x}{3}$=$\frac{3}{x}$•$\frac{3}{x}$=$\frac{9}{{x}^{2}}$���ʴ�ѡ�����
B����$\frac{1}{x-3}-\frac{x+1}{{x}^{2}-1}$��•��x-3��
=$\frac{1}{x-3}$����x-3��-$\frac{x+1}{��x+1����x-1��}$����x-3��
=1-$\frac{1}{x-1}$����x-3��
=$\frac{2}{x-1}$���ʴ�ѡ����ȷ��
C����$\frac{a}{a-2}-\frac{a}{a+2}$��•$\frac{4-{a}^{2}}{a}$
=-��a+2��-��2-a��
=-4���ʴ�ѡ�����
D����$\frac{{b}^{2}}{a+b}-\frac{{a}^{2}}{a+b}$��•$\frac{ab}{a-b}$
=$\frac{��b+a����b-a��}{a+b}$•$\frac{ab}{a-b}$
=-ab���ʴ�ѡ�����
��ѡ��B��
���� ������Ҫ�����˷�ʽ�Ļ�����㣬��ȷ�����ʽ�ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
13������$\frac{5{x}^{3}y}{15{x}^{2}{y}^{2}}$�Ľ����������
| A�� | $\frac{x}{10y}$ | B�� | $\frac{{x}^{3}y}{10{x}^{2}{y}^{2}}$ | C�� | $\frac{x}{3y}$ | D�� | $\frac{{x}^{3}y}{3{x}^{2}{y}^{2}}$ |
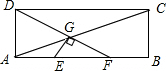 ��ͼ������ABCD�У�AB=3AD��E��F��AB�ϣ���AE=EF=FB��AC��DF��G������EG����֤��EG��DF��
��ͼ������ABCD�У�AB=3AD��E��F��AB�ϣ���AE=EF=FB��AC��DF��G������EG����֤��EG��DF��