题目内容
如图，△ABC内接于⊙O，AD为⊙O的直径，交BC于点E，若DE=2，OE=3，则tanC•tanB=（ ）
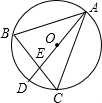
| A．2 | B．3 | C．4 | D．5 |
连接BD、CD，由圆周角定理可知∠B=∠ADC，∠C=∠ADB，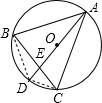
∴△ABE∽△CDE，△ACE∽△BDE，
∴
=
=
，
=
=
，
由AD为直径可知∠DBA=∠DCA=90°，
∵DE=2，OE=3，
∴AO=OD=OE+ED=5，AE=8，
tanC•tanB=tan∠ADB•tan∠ADC=
•
=
•
=
•
=
•
=
=
=4．
故选C．
∴△ABE∽△CDE，△ACE∽△BDE，
∴
| AB |
| CD |
| BE |
| DE |
| AE |
| CE |
| AC |
| BD |
| CE |
| DE |
| AE |
| BE |
由AD为直径可知∠DBA=∠DCA=90°，
∵DE=2，OE=3，
∴AO=OD=OE+ED=5，AE=8，
tanC•tanB=tan∠ADB•tan∠ADC=
| AB |
| BD |
| AC |
| CD |
| BE |
| DE |
| CE |
| DE |
| AB |
| CD |
| AC |
| BD |
| AE |
| CE |
| CE |
| DE |
| AE |
| DE |
| 8 |
| 2 |
故选C．
练习册系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
