题目内容
1.若一个等腰三角形的两边长分别是3cm和5cm,求它的周长.分析 题目给出等腰三角形有两条边长为3cm和5cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解答 解:分两种情况:
当三边是3,3,5时,能构成三角形,则周长是11;
当三边是3,5,5时,能构成三角形,则周长是13.
所以等腰三角形的周长为11cm或13cm.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.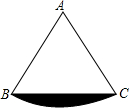 如图,正△ABC的边长为3,以A为圆心,AB为半径作弧,则图中阴影部分的面积是( )
如图,正△ABC的边长为3,以A为圆心,AB为半径作弧,则图中阴影部分的面积是( )
 如图,正△ABC的边长为3,以A为圆心,AB为半径作弧,则图中阴影部分的面积是( )
如图,正△ABC的边长为3,以A为圆心,AB为半径作弧,则图中阴影部分的面积是( )| A. | $π-\frac{3\sqrt{3}}{4}$ | B. | $\frac{3π}{2}-\frac{9\sqrt{3}}{2}$ | C. | $\frac{3π}{2}$-$\frac{9\sqrt{3}}{4}$ | D. | 3$π-\frac{9\sqrt{3}}{4}$ |
11.对于反比例函数y=$\frac{2}{x}$,下列说法正确的是( )
| A. | 图象经过点(-2,1) | B. | 图象位于第二、第四象限 | ||
| C. | y随x的增大而减小 | D. | 当x>1时,0<y<2 |
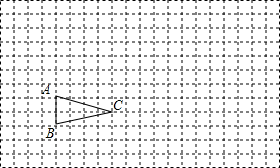 作图题:如图所示,△ABC在方格纸中
作图题:如图所示,△ABC在方格纸中