题目内容
15.解方程:(1)x2+x-1=0;
(2)x2+3x-1=0.
分析 (1)先找出a,b,c,求出△=b2-4ac的值,再代入求根公式即可求得;
(2)先找出a,b,c,求出△=b2-4ac的值,再代入求根公式求得即可.
解答 解:(1)x2+x-1=0;
∵a=1,b=1,c=-1,△=b2-4ac=1+4=5,
∴x=$\frac{-1±\sqrt{5}}{1×2}$=$\frac{-1±\sqrt{5}}{2}$.
即x1=$\frac{-1+\sqrt{5}}{2}$,x2=$\frac{-1-\sqrt{5}}{2}$.
(2)x2+3x-1=0.
∵a=1,b=3,c=-1,△=b2-4ac=9+4=13,
∴x=$\frac{-3±\sqrt{13}}{1×2}$=$\frac{-3±\sqrt{13}}{2}$.
即x1=$\frac{-3+\sqrt{13}}{2}$,x2=$\frac{-3-\sqrt{13}}{2}$.
点评 本题考查了用公式法解一元二次方程,找出a,b,c,求出△=b2-4ac的值,是解此题的关键.

练习册系列答案
相关题目
6.下列各组数中,数值相等的是( )
| A. | 23和32 | B. | -53和(-5)3 | C. | (-$\frac{2}{3}$)2和(-$\frac{3}{2}$)2 | D. | (-3)4和(-4)3 |
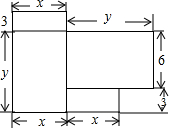 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).