Question

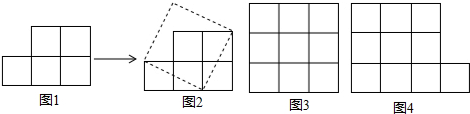
如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．

（1）拼成的正方形的面积与边长分别是多少？

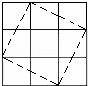
（2）你能在3×3方格图中，连接四个点组成面积为5的正方形吗？

（3）你能把十个小正方形组成的图形纸，剪开并拼成正方形吗？若能，则它的边长是多少？

Answer 1

考点：

剪纸问题；勾股定理．.

分析：

（1）一共有5个小正方形，那么组成的大正方形的面积为5，边长为5的算术平方根；

（2）根据面积公式求出边长是 ，根据勾股定理1²+2²=5，画出正方形即可；

（3）一共有10个小正方形，那么组成的大正方形的面积为10，边长为10的算术平方根，在所给图形中截取两条长为 的且互相垂直的线段，进而拼合即可．

解答：

解：（1）5个小正方形拼成一个大正方形后，面积不变，所以拼成的正方形的面积是：5×1×1=5

边长=

（2）能．如图所示：

（3）能，如图所示：

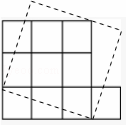
边长=

点评：

本题考查了勾股定理，正方形的面积和正方形的有关画图，巧妙地根据网格的特点画出正方形是解此题的关键．正方形的面积是由组成正方形的面积的小正方形的个数决定的；边长为面积的算术平方根．