题目内容
16.反比例函数y=$\frac{\sqrt{3}}{x}$图象上有两个点(x1,y1),(x2,y2),其中x1<x2<0,则y1,y2的大小关系是y1>y2.分析 根据反比例函数的增减性进行判断即可.
解答 解:
在y=$\frac{\sqrt{3}}{x}$中,
∵k=$\sqrt{3}$>0,
∴函数图象在第一、三象限,且在每个象限内y随x的增大而减小,
∵x1<x2<0,
∴y1>y2,
故答案为:y1>y2.
点评 本题主要考查反比例函数的增减性,掌握反比例函数的性质是解题的关键,即在y=$\frac{k}{x}$(k≠0)中,当k>0时,函数图象在第一、三象限,且在每个象限内y随x的增大而减小,当k<0时,函数图象在第二、四郇象限,且在每个象限内y随x的增大而增大.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
7.一个不透明的盒子中装有5个红球和3个白球,它们除颜色外都相同.若从中任意摸出一个球,则下列叙述正确的是( )
| A. | 摸到红球是必然事件 | B. | 摸到白球是不可能事件 | ||
| C. | 摸到红球比摸到白球的可能性相等 | D. | 摸到红球比摸到白球的可能性大 |
11.在反比例函数y=-$\frac{1}{x}$的图象上有三点A(-2,a),B(-1,b),C(3,c),则a,b,c的大小关系是( )
| A. | b<c<a | B. | c<a<b | C. | c<b<a | D. | a<b<c |
1.下列算式正确的是( )
| A. | $\sqrt{25}$=±5 | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{18}$÷$\sqrt{2}$=9 | D. | $\sqrt{12}$•$\sqrt{\frac{1}{3}}$=2 |
6.抛物线y=-2x2-6x+1与x轴的交点个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
 如图,求等腰三角形ABC的面积.
如图,求等腰三角形ABC的面积.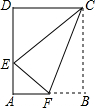 如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$.
如图,矩形纸片ABCD中,AD=5,CD=4,把这张矩形纸片沿着直线CF折叠后顶点B恰好落在边AD上的点E处,则BF的长为$\frac{5}{2}$.