题目内容
14. 如图所示分别以直角三角形的两直角边AB,AC及斜边BC为直径向外作半圆,AB=4cm,AC=3cm,BC=5cm.求阴影部分的面积.
如图所示分别以直角三角形的两直角边AB,AC及斜边BC为直径向外作半圆,AB=4cm,AC=3cm,BC=5cm.求阴影部分的面积.
分析 分别求出以AB、AC、BC为直径的半圆及△ABC的面积,再根据S阴影=S1+S2+S△ABC-S3即可得出结论.
解答 解:∵∠BAC=90°,AB=4cm,AC=3cm,BC=5cm,
∴以AB为直径的半圆的面积S1=2π(cm2);
以AC为直径的半圆的面积S2=$\frac{9}{8}$π(cm2);
以BC为直径的半圆的面积S3=$\frac{25}{8}$π(cm2);
S△ABC=6(cm2);
∴S阴影=S1+S2+S△ABC-S3=6(cm2).
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
4.一个直角三角形一直角边长为6,另一直角边长为8,则斜边长为( )
| A. | 6 | B. | 8 | C. | 2$\sqrt{7}$ | D. | 10 |
2. 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
 如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )
如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=58°,则∠AOC等于( )| A. | 58° | B. | 42° | C. | 32° | D. | 22° |
19.若a>b,则下列式子正确的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | $\frac{3-a}{2}$>$\frac{3-b}{2}$ | D. | a+3b<4b |
4.已知直线y=kx+b与y=2x-5平行且经过点(1,3),则y=kx+b的表达式是( )
| A. | y=x+2 | B. | y=2x+1 | C. | y=2x+2 | D. | y=2x+3 |
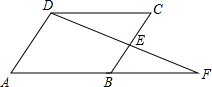 如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F.
如图,在菱形ABCD中,点E是BC的中点,连接DE并延长与AB的延长线交于点F. 如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连接CD,DE.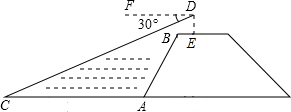 如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)
如图,小明站在河岸上的E点,看见正对面的河岸边有一点C,此时测得C点的俯角是30°.若小明的眼睛与地面的距离DE是1.6米,BE=1米,BE平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求河宽AC.(结果保留整数,参考数据:$\sqrt{3}$≈1.73)