题目内容
15. 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有1小时.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终到达C港,设甲乙两船行驶的时间为x(h),与B港的距离为y(km),它们间的函数关系如图所示,若两船的距离不超过10km时能够相互望见,则甲乙两船可以互相望见的时间共有1小时.
分析 由图象可求出甲、乙两船的速度为60千米/时,30千米/时,则甲、乙两船离A港口的距离为S甲=60x,S乙=30x+30,有三种可能:①S乙-S甲=10,②S甲-S乙=10;③120-S乙=10,将甲、乙的函数关系式代入分别求x,得出x的取值范围,进而求解即可.
解答 解:由图象可知,
甲船的速度为:30÷0.5=60千米/时,
乙船的速度为:90÷3=30千米/时,
由此可得:
所以,甲、乙两船离A港口的距离为S甲=60x,S乙=30x+30,
①当乙船在甲船前面10千米时,S乙-S甲=10,
即:30x+30-60x=10,解得x=$\frac{2}{3}$,
②当甲船在乙船前面10千米时,S甲-S乙=10,
即:60x-(30x+30)=10,解得x=$\frac{4}{3}$,
所以,当$\frac{2}{3}$≤x≤$\frac{4}{3}$时,甲、乙两船可以相互望见;
③由图可知,A、B两港相距30km,B、C两港相距90km,A、C两港相距120km,
甲船到达C港需要的时间:120÷60=2小时,乙船到达C港需要的时间:90÷30=3小时,
当2≤x≤3时,甲船已经到了而乙船正在行驶,
两船的距离是10km,即乙船与C港的距离是10km,
即:120-(30x+30)=10,解得x=$\frac{8}{3}$,
所以,当$\frac{8}{3}$≤x≤3时,甲、乙两船可以相互望见;
($\frac{4}{3}$-$\frac{2}{3}$)+(3-$\frac{8}{3}$)=1小时.
故答案为1.
点评 本题考查了一次函数的应用.关键是根据图象求出甲乙两船的行驶速度,再表示两船离A港口的距离,分类列出方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.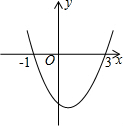 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=-1,x2=3.
其中正确的是( )
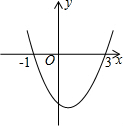 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有如下结论:①a>0;②b>0;③a+b+c>0;④2a+b=0;⑤方程ax2+bx+c=0的解为x1=-1,x2=3.
其中正确的是( )
| A. | ①②③ | B. | ②③④ | C. | ③④⑤ | D. | ①④⑤ |
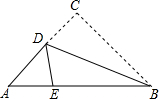 如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.
如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.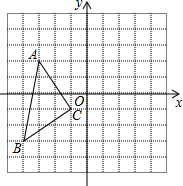 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积.
如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论正确的有( )
 已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.
已知抛物线y=ax2+bx+c(a<0)经过点A(-3,0)、B(1,0),且与y轴交于点C,设抛物线的顶点为D.