题目内容
已知AB为⊙O的直径AC、AD为⊙O的弦,若AB=2AC= AD,则∠DBC的度数为 ????????????
AD,则∠DBC的度数为 ????????????
【答案】
15°或75°.
【解析】
试题分析:当点C、D在直径AB的异侧时,
∵AB为直径,
∴∠ACB=∠ADB=90°,
∵AB=2AC,
∴sin∠ABC=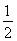 ,
,
∴∠ABC=30°,
∵AB=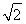 AD
AD
∴AD=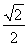 AB,
AB,
∴∠ABD=45°
∴∠DBC=∠ABC+∠ABD=30°+45°=75°;
当点C、D在直径AB的同侧时,
同理可得,∠DBC=∠ABD﹣∠ABC=45°﹣30°=15°.
故答案是15°或75°.
考点:垂径定理.

练习册系列答案
相关题目
 如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°. 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )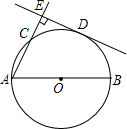 如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线.
如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线. (2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.
(2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC. 已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.