题目内容
5. 如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,E为AC的中点,连接DE,当线段AB=4,∠ACB=60°时,△CED周长是2$\sqrt{3}$+4.
如图,已知线段AB,分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,连接AC,BC,E为AC的中点,连接DE,当线段AB=4,∠ACB=60°时,△CED周长是2$\sqrt{3}$+4.
分析 由作图的过程可知CQ是线段AB的垂直平分线,所以可得D为AB中点,结合已知条件可得DE是△ABC的中位线,所以DE的长可求出,再由勾股定理可求出CD的长,由E是AC的中点可求出CE的长,进而可求出△CED的周长.
解答 解:
∵分别以A、B为圆心,大于$\frac{1}{2}$AB长为半径画弧,两弧相交于点C、Q,连接CQ与AB相交于点D,
∴CQ是线段AB的垂直平分线,
∴CA=CB,
∵∠ACB=60°,
∴△ACB是等边三角形,
∴AC=AB=BC=4,
∴CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵E为AC的中点,D是AB中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=2,
∴△CED周长=2+2+2$\sqrt{3}$=4+2$\sqrt{3}$.
故答案为:4+2$\sqrt{3}$.
点评 本题考查了基本作图中作已知线段的垂直平分线及线段的垂直平分线的性质,能够判定△ACB是等边三角形是解题的关键,题目难度不大.

练习册系列答案
相关题目
10.下列各式中是一次函数的是( )
| A. | y=2(x-6)2 | B. | y=2(x-6) | C. | y=$\frac{2}{x-6}$ | D. | 2(x-6)=0 |
 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,∠A与∠D的关系为∠A=2∠D.
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D,∠A与∠D的关系为∠A=2∠D. 如图,已知函数y1=kx-1和y2=x-b的图象交于点P(-2,-5),则根据图象可得不等式kx-1>x-b的解集是x>-2.
如图,已知函数y1=kx-1和y2=x-b的图象交于点P(-2,-5),则根据图象可得不等式kx-1>x-b的解集是x>-2.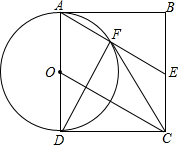 如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.
如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.