��Ŀ����
��ͼ�����κ���y= ?x2axb��ͼ����x�ύ��A��?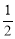 ��0����B��2��0�����㣬����y�ύ�ڵ�C.
��0����B��2��0�����㣬����y�ύ�ڵ�C.
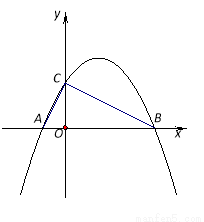
��1����Ò����ߵĽ���ʽ�����жϡ�ABC����״��
��2����x���Ϸ��Ē���������һ��D������A��C��D��B�ĵ�Ϊ������ı����ǵ������Σ���ֱ��д��D������ꣻ
��3���ڒ������ϴ��ڵ�P��ʹ����A��C��B��P�ĵ�Ϊ������ı�����ֱ�����Σ����P�������.
��1��y=-x2+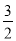 x+1����ABC��ֱ�������Σ��ҡ�ACB=90�㣻��2��D��
x+1����ABC��ֱ�������Σ��ҡ�ACB=90�㣻��2��D��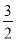 ��1������3��P��
��1������3��P��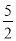 ��-
��-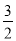 ����-
����-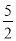 ��-9��.
��-9��.
��������
�����������1����A��B��������������ߵĽ���ʽ�м���ȷ�������ߵĽ���ʽ�������ɵõ�C�����꣬���������AC��BC��AB�ij���Ȼ�����жϡ�ABC����״��
��2�����������ߺ͵������εĶԳ���֪����C���������߶Գ���ĶԳƵ���ϵ�D��Ҫ���ɴ˿������D�����ꣻ
��3���ڣ�1�����ѽ�֤�á�ACB=90�㣬��A��C��B��P�ĵ�Ϊ������ı�����ֱ�����Σ��������������Ҫ���ǣ�
����BC��APΪ�ף�ACΪ�ߣ��������ֱ��BC�Ľ���ʽ��������ȷ��ֱ��AP�Ľ���ʽ�����������ߵĽ���ʽ���������P�����꣮
����AC��BPΪ�ף�BCΪ�ߣ�����ͬ�٣�
�����������1��������ã�
 ��
��
���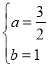 ��
��
�������ߵĽ���ʽΪy=-x2+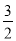 x+1��
x+1��
��C��0��1����
��AC2=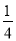 +1=
+1=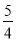 ��BC2=1+4=5��AB2=��2+
��BC2=1+4=5��AB2=��2+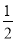 ��2=
��2=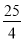 ��
��
��AC2+BC2=AB2������ABC��ֱ�������Σ��ҡ�ACB=90�㣻
��2���ɣ�1����������֪����Գ��᷽��Ϊx=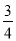 ��
��
���������ߺ͵������εĶԳ���֪����D��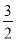 ��1����
��1����
��3�����ڣ���P��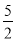 ��-
��-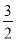 ����-
����-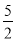 ��-9����
��-9����
����A��C��B��P�ĵ�Ϊ�����ֱ��������BC��APΪ�ף�
��B��2��0����C��0��1����
��ֱ��BC�Ľ���ʽΪ��y=-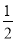 x+1��
x+1��
�����A��ƽ����BC��ֱ�ߵĽ���ʽΪy=-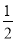 x+h��
x+h��
������-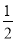 ������-
������-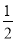 ��+h=0��h=-
��+h=0��h=-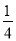 ��
��
��y=-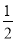 x-
x-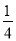 ��
��
���������ߵĽ���ʽ�У�
 ��
��
���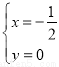 ��
��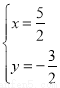 ��
��
���P��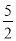 ��-
��-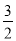 ����
����
����A��C��B��P�ĵ�Ϊ�����ֱ��������AC��BPΪ�ף�
ͬ�������P��-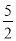 ��-9����
��-9����
�ʵ�P��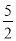 ��-
��-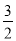 ����-
����-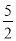 ��-9��ʱ����A��C��B��P�ĵ�Ϊ������ı�����ֱ�����Σ�
��-9��ʱ����A��C��B��P�ĵ�Ϊ������ı�����ֱ�����Σ�
�����������ߵĶԳ��������һ��P��������ɣ�
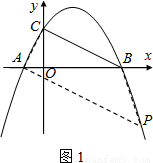
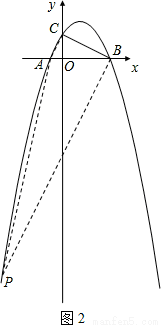
���㣺���κ����ۺ��⣮



 D��
D��
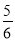 ��
��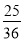 ��һ��ƽ����
��һ��ƽ����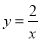 ��
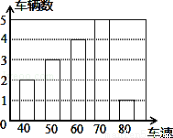
��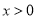 ����ͼ���ϣ��е�
����ͼ���ϣ��е�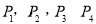 �����ǵĺ���������Ϊ1��2��3��4���ֱ����Щ����
�����ǵĺ���������Ϊ1��2��3��4���ֱ����Щ����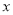 ����
����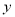 ��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������Ϊ
��Ĵ��ߣ�ͼ�������ɵ���Ӱ���ֵ��������������Ϊ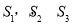 ����
����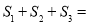 ��
��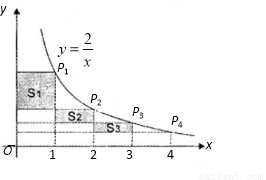
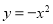 ����ƽ��1����λ��Ȼ������ƽ��3����λ����ƽ�ƺ������ߵĽ���ʽΪ�� ��. A��
����ƽ��1����λ��Ȼ������ƽ��3����λ����ƽ�ƺ������ߵĽ���ʽΪ�� ��. A��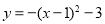
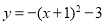
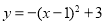
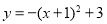

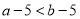 B��
B�� C��
C�� D��
D��