题目内容
1.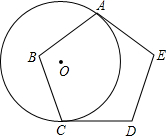 如图,半径为1的圆O与正五边形ABCDE相切于点A、C,劣弧AC的长度为( )
如图,半径为1的圆O与正五边形ABCDE相切于点A、C,劣弧AC的长度为( )| A. | $\frac{3}{5}$π | B. | $\frac{4}{5}$π | C. | $\frac{3}{4}$π | D. | $\frac{2}{3}$π |
分析 先求得正五边形的内角的度数,然后根据弧长公式即可求得.
解答  解:因为正五边形ABCDE的内角和是(5-2)×180=540°,
解:因为正五边形ABCDE的内角和是(5-2)×180=540°,
则正五边形ABCDE的一个内角=$\frac{540°}{5}$=108°;
连接OA、OB、OC,
∵圆O与正五边形ABCDE相切于点A、C,
∴∠OAE=∠OCD=90°,
∴∠OAB=∠OCB=108°-90°=18°,
∴∠AOC=144°
所以劣弧AC的长度为$\frac{144π×1}{180}$=$\frac{4}{5}$π.
故选B.
点评 本题考查了正五边形的内角和的计算以及弧长的计算,难度适中.

练习册系列答案
相关题目
11.下列无理数中,在-1与2之间的是( )
| A. | -$\sqrt{3}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
10.下列计算中正确的是( )
| A. | a2+a3=2a5 | B. | (a2)3=a5 | C. | (ab2)3=ab6 | D. | a2•a3=a5 |
 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.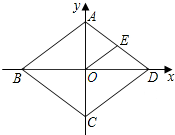 如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标(5,0)(-5,0)(8,0)($\frac{25}{8}$,0).
如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标(5,0)(-5,0)(8,0)($\frac{25}{8}$,0).