题目内容
5. 在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数y=$\frac{k}{x}$(k>0)在第一象限内过点A,且与BC交于点F.当F为BC的中点,且S△AOF=24$\sqrt{3}$时,点C的坐标为(10$\sqrt{2}$,4$\sqrt{6}$).
在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数y=$\frac{k}{x}$(k>0)在第一象限内过点A,且与BC交于点F.当F为BC的中点,且S△AOF=24$\sqrt{3}$时,点C的坐标为(10$\sqrt{2}$,4$\sqrt{6}$).
分析 先设OA=a(a>0),过点F作FM⊥x轴于M,根据∠AOB=60°,得出AHAH=$\frac{\sqrt{3}}{2}$a,OH=$\frac{1}{2}$a,求出S△AOH的值,根据S△AOF=24$\sqrt{3}$,求出平行四边形AOBC的面积,根据F为BC的中点,求出S△OBF=12$\sqrt{3}$,最后根据S平行四边形AOBC=OB•AH,得出OB=AC=12,即可求出点C的坐标;
解答 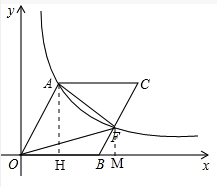 解:设OA=a(a>0),过点F作FM⊥x轴于M,
解:设OA=a(a>0),过点F作FM⊥x轴于M,
∵∠AOB=60°,
∴AH=$\frac{\sqrt{3}}{2}$a,OH=$\frac{1}{2}$a,
∴S△AOH=$\frac{1}{2}$•$\frac{\sqrt{3}}{2}$a•$\frac{1}{2}$a=$\frac{\sqrt{3}}{8}$a2,
∵S△AOF=24$\sqrt{3}$,
∴S平行四边形AOBC=48$\sqrt{3}$,
∵F为BC的中点,
∴S△OBF=12$\sqrt{3}$,
∵BF=$\frac{1}{2}$a,∠FBM=∠AOB,
∴FM=$\frac{\sqrt{3}}{4}$,BM=$\frac{1}{4}$a,
∴S△BMF=$\frac{1}{2}$BM•FM=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$×$\frac{1}{4}$a=$\frac{\sqrt{3}}{32}$a2,
∴S△FOM=S△OBF+S△BMF=12$\sqrt{3}$+$\frac{\sqrt{3}}{32}$a2,
∵点A,F都在y=$\frac{k}{x}$的图象上,
∴S△AOH=$\frac{1}{2}$k,
∴$\frac{\sqrt{3}}{8}$a2=12$\sqrt{3}$+$\frac{\sqrt{3}}{32}$a2,
∴a=8$\sqrt{2}$,
∴OA=8$\sqrt{2}$,
∴OH=4$\sqrt{2}$,AH=$\sqrt{3}$OH=$\sqrt{3}$×4$\sqrt{2}$=4$\sqrt{6}$,
∵S平行四边形AOBC=OB•AH=48$\sqrt{3}$,
∴OB=AC=6$\sqrt{2}$,
∴C(10$\sqrt{2}$,4$\sqrt{6}$).
故答案为:(10$\sqrt{2}$,4$\sqrt{6}$).
点评 此题考查了反比例函数的综合,用到的知识点是三角函数、平行四边形、反比例函数、三角形的面积等,要注意运用数形结合的思想,

| A. | 王华期末考试数学成绩会是100分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球 |
 如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1.
如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1.