题目内容
19.关于x,y的方程组$\left\{\begin{array}{l}{2x-y=m}\\{x+my=n}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,则|m-n|的值是1.分析 先把x=1,y=1代入方程,可得关于m,n的方程组,解答后代入|m-n|即可.
解答 解:把x=1,y=1代入方程$\left\{\begin{array}{l}{2x-y=m}\\{x+my=n}\end{array}\right.$,
可得:$\left\{\begin{array}{l}{2-1=m}\\{1+m=n}\end{array}\right.$,
解得:m=1,n=2,
把m=1,n=2代入|m-n|=1,
故答案为:1.
点评 本题考查了二元一次方程的解,解题的关键是掌握加减消元的思想.

练习册系列答案
相关题目
10.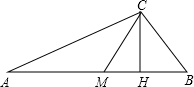 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )| A. | AB2=AC2+BC2 | B. | CH2=AH•HB | C. | CM=$\frac{1}{2}$AB | D. | CB=$\frac{1}{2}$AB |
 (1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.
(1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.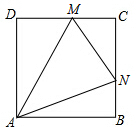 如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.
如图:已知正方形ABCD,动点M、N分别在DC、BC上,且满足∠MAN=45°,△CMN的周长为2,则△CMN面积的最大值是3-2$\sqrt{2}$.