题目内容
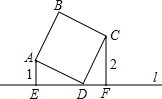 如图,直线l过正方形ABCD的顶点D,点A、C到直线l的距离分别是1和2,则正方形ABCD的面积为( )
如图,直线l过正方形ABCD的顶点D,点A、C到直线l的距离分别是1和2,则正方形ABCD的面积为( )分析:根据正方形性质得出AD=CD,∠ADC=90°,求出∠EAD=∠FDC,证△AED≌△DFC,求出DE=CF=2,在Rt△AED中,由勾股定理求出AD,即可求出正方形的面积.
解答:解:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AED=∠DFC=90°,
∴∠ADE+∠CDF=180°-90°=90°,∠ADE+∠EAD=90°,
∴∠EAD=∠CDF,
∵在△AED和△DFC中
,
∴△AED≌△DFC(AAS),
∴DE=CF=2,
在Rt△AED中,由勾股定理得:AD=
=
,
即正方形ABCD的面积是(
)2=5.
故选D.
∴AD=CD,∠ADC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AED=∠DFC=90°,
∴∠ADE+∠CDF=180°-90°=90°,∠ADE+∠EAD=90°,
∴∠EAD=∠CDF,
∵在△AED和△DFC中
|
∴△AED≌△DFC(AAS),
∴DE=CF=2,
在Rt△AED中,由勾股定理得:AD=
| 12+22 |
| 5 |
即正方形ABCD的面积是(
| 5 |
故选D.
点评:本题考查了正方形性质,全等三角形的性质和判定,勾股定理的应用,关键是求出DE=CF,主要考查学生分析问题和解决问题的能力,题型较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
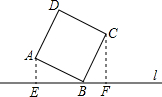 如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )
如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和2,则正方形的边长是( )| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
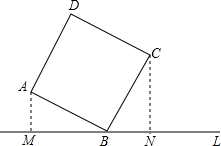 如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是
如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是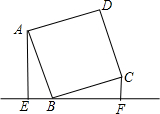 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别是a和b,则正方形的边长是 15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为
15、如图,直线l过正方形ABCD的顶点D,过A、C分别作直线l的垂线,垂足分别为E、F.若AE=4a,CF=a,则正方形ABCD的面积为 如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是
如图,直线d过正方形ABCD的顶点B,点A,C到直线d的距离分别是