题目内容
8.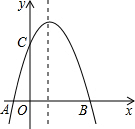 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;
(2)若在该抛物线的对称轴上存在一点P,使得PC=PB,请求出符合条件的点P的坐标,并说明理由.
分析 (1)根据A、B、C三点的坐标可以求得抛物线的解析式;
(2)由点P在抛物线的对称轴上,由第一问中可求得抛物线的对称轴,从而可知点P的横坐标,根据PC=PB可以求得点P的坐标.
解答 解:(1)∵抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3),设抛物线的解析式为y=ax2+bx+c,
∴$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得a=-1,b=2,c=3.
∴抛物线的解析式为:y=-x2+2x+3.
(2)点P的坐标为(1,1).
理由:由(1)知抛物线的解析式为:y=-x2+2x+3,
∴抛物线的对称轴为:x=-$\frac{2}{2×(-1)}$=1.
∵点P在抛物线的对称轴上,设点P的坐标为(1,y),
又∵PC=PB,B(3,0),C(0,3),
∴$\sqrt{(3-y)^{2}+(0-1)^{2}}$=$\sqrt{(0-y)^{2}+({3-1)}^{2}}$.
解得y=1.
故点P的坐标为(1,1).
点评 本题考查求抛物线的解析式和探究性问题,关键是明确题意,进行正确分析,从而解答本题.

练习册系列答案
相关题目
13.在数轴上有一点M表示的数是3,而点N与点M的距离是2个单位长度,则点N所表示数是( )
| A. | -2 | B. | 1 | C. | 5 | D. | 1或5 |
20.若二次函数y=x2+bx的图象的对称轴是经过点(3,0)且平行于y轴的直线,则关于x的方程x2+bx=7的解为( )
| A. | x1=0,x2=6 | B. | x1=1,x2=7 | C. | x1=1,x2=-7 | D. | x1=-1,x2=7 |
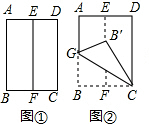 将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.
将长方形纸片ABCD按如下顺序进行折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③);请你求出图②中∠BCB′的度数.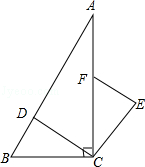 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF. 如图所示,在长和宽分别是a,9的长方形纸片的四个角都剪去一个边长为x的正方形.
如图所示,在长和宽分别是a,9的长方形纸片的四个角都剪去一个边长为x的正方形.