题目内容
为落实国家“三农”政策,某地政府组织40辆汽车装运A、B、C三种农产品共200吨到外地销售,按计划,40辆车都要装运,每辆车只能装运同一种农产品,且必须装满,根据下表提供的信息,解答下列问题:
| 农产品种类 | A | B | C |
| 每辆汽车的装载量(吨) | 4 | 5 | 6 |
(1)如果装运C种农产品需13辆汽车,那么装运A、B两种农产品各需多少辆汽车?
(2)如果装运每种农产品至少需要11辆汽车,那么车辆的装运方案有几种?写出每种装运方案.
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【专题】应用题.
【分析】(1)设装运A、B两种农产品各需x、y辆汽车.等量关系:40辆车都要装运,A、B、C三种农产品共200吨;
(2)关系式为:装运每种农产品的车辆数≥11.
【解答】解:(1)设装运A、B两种农产品各需x、y辆汽车.则

 ,
,
解得
 .
.
答:装运A、B两种农产品各需13、14辆汽车;
(2)设装运A、B两种农产品各需a、b辆汽车.则
4a+5b+6(40﹣a﹣b)=200,
解得:b=﹣2a+40.
由题意可得如下不等式组:
 ,
,
解得:11≤a≤14.5
因为a是正整数,
所以a的值可为11,12,13,14共4个值,因而有四种安排方案.
方案一:11车装运A,18车装运B,11车装运C
方案二:12车装运A,16车装运B,12车装运C.
方案三:13车装运A,14车装运B,13车装运C.
方案四:14车装运A,12车装运B,14车装运C.
【点评】本题考查了二元一次方程组和一元一次不等式组的应用,解决本题的关键是读懂题意,根据关键描述语,找到所求量的等量关系,确定x的范围,得到装载的几种方案是解决本题的关键.

练习册系列答案
相关题目
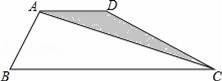

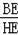
 =
=
 ;③CD=2DH;④
;③CD=2DH;④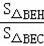
 =
=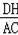




 ﹣|
﹣| |﹣4
|﹣4 +
+ .
.