题目内容
5. 如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为4.
如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=$\sqrt{3}$,那么当点P运动一周时,点Q运动的总路程为4.
分析 首先根据题意正确画出从O→B→A运动一周的图形,分四种情况进行计算:①点P从O→B时,路程是线段PQ的长;②当点P从B→C时(QC⊥AB,C为垂足),点Q从O运动到Q,计算OQ的长就是运动的路程;③点P从C→A时,点Q由Q向左运动,路程为QQ′;④点P从A→O时,点Q运动的路程就是点P运动的路程;最后相加即可.
解答  解:在Rt△AOB中,∵∠ABO=30°,AO=1,
解:在Rt△AOB中,∵∠ABO=30°,AO=1,
∴AB=2,BO=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
①当点P从O→B时,如图1、图2所示,点Q运动的路程为$\sqrt{3}$,
②如图3所示,QC⊥AB,则∠ACQ=90°,即PQ运动到与AB垂直时,垂足为P,
当点P从B→C时,
∵∠ABO=30°
∴∠BAO=60°
∴∠OQD=90°-60°=30°
∴cos30°=$\frac{CQ}{AQ}$
∴AQ=$\frac{CQ}{cos30°}$=2
∴OQ=2-1=1
则点Q运动的路程为QO=1,
③当点P从C→A时,如图3所示,点Q运动的路程为QQ′=2-$\sqrt{3}$,
④当点P从A→O时,点Q运动的路程为AO=1,
∴点Q运动的总路程为:$\sqrt{3}$+1+2-$\sqrt{3}$+1=4
故答案为:4
点评 本题主要是应用三角函数定义来解直角三角形,此题的解题关键是理解题意,正确画出图形;线段的两个端点看成是两个动点,将线段移动问题转化为点移动问题.

练习册系列答案
相关题目
15.下列实数中$\sqrt{7}$,-(-π),|-3|,3中,最大的是( )
| A. | $\sqrt{7}$ | B. | -(-π) | C. | |-3| | D. | 3 |
16.用一枚直径为25mm的硬币完全覆盖一个正六边形,则这个正六边形的最大边长是( )
| A. | $\frac{25}{2}$mm | B. | $\frac{25}{2}$$\sqrt{3}$mm | C. | $\frac{25}{4}$mm | D. | $\frac{25}{4}$$\sqrt{3}$mm |
10.不等式x+7<3x+1的解集是( )
| A. | x<-3 | B. | x>3 | C. | x<-4 | D. | x>4 |
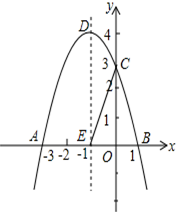 如图,关于y=-x2+bx+c的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,点E在x轴上.
如图,关于y=-x2+bx+c的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,点E在x轴上.

 如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.