题目内容
10.化简:$\frac{2x}{x+1}$-$\frac{2x+4}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$,然后在不等式组$\left\{\begin{array}{l}{2x-2<x}\\{3-\frac{x}{3}>\frac{4}{3}}\end{array}\right.$的非负整数解中选择一个适当的数代入求值.分析 首先利用分式的混合运算法则将原式化简,然后解不等式组,选择使得分式有意义的值代入求解即可求得答案.
解答 解:$\frac{2x}{x+1}$-$\frac{2x+4}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$
=$\frac{2x}{x+1}$-$\frac{2(x+2)}{(x+1)(x-1)}$×$\frac{(x-1)^{2}}{x+2}$
=$\frac{2x}{x+1}$-$\frac{2(x-1)}{x+1}$
=$\frac{2x-2(x-1)}{x+1}$
=$\frac{2}{x+1}$,
∵不等式组$\left\{\begin{array}{l}{2x-2<x}\\{3-\frac{x}{3}>\frac{4}{3}}\end{array}\right.$的解集为x<2,x<2的非负整数解是0,1,
∵(x+1)(x-1)≠0,x+2≠0,
∴x≠±1,x≠-2,
∴把x=0代入$\frac{2}{x+1}$=2.
点评 此题考查了一元一次不等式组的整数解,分式的化简求值问题.注意掌握分式有意义的条件是解此题的关键.

练习册系列答案
相关题目
20.下列事件中属于随机事件的是( )
| A. | 抛掷一石头,石头终将落地 | B. | 从装有黑球,白球的袋里摸出红球 | ||
| C. | 太阳绕着地球转 | D. | 买1张彩票,中500万大奖 |
1.计算(-3)+(-9)的结果是( )
| A. | +6 | B. | -6 | C. | -12 | D. | 12 |
19.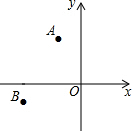 如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
 如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-4,8),B(-10,-3),以原点O为位似中心,相似比为$\frac{1}{2}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-2,4) | B. | (-8,16) | C. | (-2,4)或(2,-4) | D. | (-8,16)或(8,-16) |
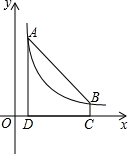 如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.