题目内容
8.先化简,再求值:(1-$\frac{x}{x-1}$)÷$\frac{x}{{x}^{2}-1}$,其中x满足x2+3x-4=0.分析 先算括号里面的,再算除法,最后求出x的值代入进行计算即可.
解答 解:原式=$-\frac{x+1}{x}$,
解x2+3x-4=0得x1=-4,x2=1.
因为x≠1,
所以当x=-4时,原式=$-\frac{3}{4}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
18.下列代数式$\frac{y}{2}$、x、$\frac{1}{3π}$、$\frac{1}{a-1}$中,是分式的是( )
| A. | $\frac{y}{2}$ | B. | $\frac{1}{a-1}$ | C. | x | D. | $\frac{1}{3π}$ |
19.用20cm长的绳子围成一个矩形,如果这个矩形的一边长为x cm,面积是S cm2,则S与x的函数关系式为( )
| A. | S=x(20-x) | B. | S=x(20-2x) | C. | S=x(10-x) | D. | S=2x(10-x) |
13.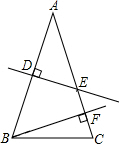 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数是( )| A. | 30° | B. | 35° | C. | 45° | D. | 36° |
20.给出下列函数:(1)y=2x;(2)y=-2x+1;(3)y=$\frac{2}{x}$.其中,y随x的增大而减小的函数是( )
| A. | (1)、(2) | B. | (1)、(3) | C. | (2)、(3) | D. | (1)、(2)、(3) |
18.下列四组等式变形中,正确的是( )
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{6}$=2,得x=$\frac{1}{3}$ | D. | 由5x=7.得x=$\frac{5}{7}$ |
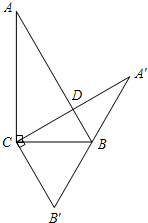 在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.
在直角△ABC中,∠C=90°,∠ABC=60°,△ABC以点C为中心旋转到△A′B′C.使B在斜边A′B′上,A′C与AB相交于D,试确定∠BDC的度数.