题目内容
解方程组:
.
|
考点:高次方程
专题:
分析:将方程②借助因式分解来降次、转化;再次联立方程①,得到两个低次方程组;解方程组即可解决问题.
解答:解:
,
由(2)得(x-2y)(y-1)=0,x-2y=0或y-1=0,
原方程可化为
.
解两个方程组得:
.
|
由(2)得(x-2y)(y-1)=0,x-2y=0或y-1=0,
原方程可化为
|
|
解两个方程组得:
|
|
|
|
点评:该题主要考查了高次方程的解法问题;解高次方程的一般策略是运用因式分解法,化高次方程为低次方程,然后求解.

练习册系列答案
相关题目
二次根式
,
,
,
,-
中,与
是同类二次根式的个数为( )
| 0.2 |
|
| 125 |
| 75 |
| 50 |
| 5 |
| A、2 | B、3 | C、4 | D、5 |
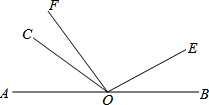 已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF=
已知点O是直线AB上的一点,∠COE=120°,射线OF是∠AOE的一条三等分线,且∠AOF=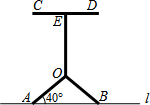 有一种小凳的示意图如图所示,支柱OE与地面l垂直,小凳表面CD与地面l平行,凳腿OA与地面l的夹角为40°,OE=35cm,OA=OB=25cm.求小凳表面CD与地面
有一种小凳的示意图如图所示,支柱OE与地面l垂直,小凳表面CD与地面l平行,凳腿OA与地面l的夹角为40°,OE=35cm,OA=OB=25cm.求小凳表面CD与地面