题目内容
已知:抛物线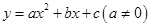 的对称轴为
的对称轴为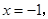 与
与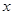 轴交于
轴交于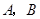 两点,与
两点,与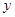 轴交于点
轴交于点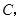 其中
其中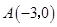 、
、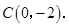
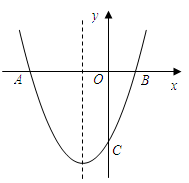
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得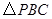 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.
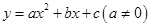 的对称轴为
的对称轴为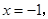 与
与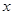 轴交于
轴交于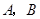 两点,与
两点,与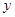 轴交于点
轴交于点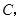 其中
其中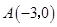 、
、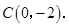

(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得
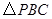 的周长最小.请求出点P的坐标.
的周长最小.请求出点P的坐标.(1)抛物线的解析式为 …………3分
…………3分
(2) 点的坐标为
点的坐标为
 …………3分
…………3分(2)
 点的坐标为
点的坐标为
(1)根据抛物线对称轴得到关于a、b的一个方程,再把点A、C的坐标代入抛物线解析式,然后解方程组求出a、b、c的值,即可得解;
(2)根据利用轴对称确定最短路线的问题,连接AC交对称轴于点P,则点P就是所求的使得△PBC的周长最小的点,然后利用待定系数法求一次函数解析式求出直线AC的解析式,再把x=-1代入直线解析式求出y的值,即可得到点P的坐标.
(2)根据利用轴对称确定最短路线的问题,连接AC交对称轴于点P,则点P就是所求的使得△PBC的周长最小的点,然后利用待定系数法求一次函数解析式求出直线AC的解析式,再把x=-1代入直线解析式求出y的值,即可得到点P的坐标.

练习册系列答案
相关题目
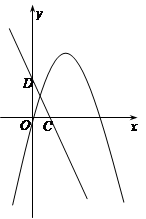
 x2+x-
x2+x-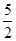 .
.
 每亩树苗的收益)
每亩树苗的收益) ,
, )
)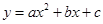 上部分点的横坐标
上部分点的横坐标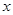 ,纵坐标
,纵坐标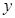 的对应值如下表:
的对应值如下表: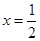 ; ④在对称轴左侧,
; ④在对称轴左侧, 图象的顶点坐标是 _ __ __.
图象的顶点坐标是 _ __ __.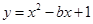 配方后为
配方后为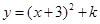 则
则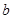 、
、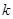 的值分别为( )
的值分别为( ) (a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程
(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程 的解为 .
的解为 . 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是
的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是 ,则a+b+c=________.
,则a+b+c=________.