Question

7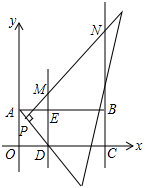．如图，在平面直角坐标系中，矩形OABC的边OA=2，OC=6，在OC上取点D将△AOD沿AD翻折，使O点落在AB边上的E点处，将一个足够大的直角三角板的顶点P从D点出发沿线段DA→AB移动，且一直角边始终经过点D，另一直角边所在直线与直线DE，BC分别交于点M，N．
（1）填空：D点坐标是（2，0），E点坐标是（2，2）；
（2）如图1，当点P在线段DA上移动时，是否存在这样的点M，使△CMN为等腰三角形？若存在，请求出M点坐标；若不存在，请说明理由．

Answer 1

分析 （1）根据△AOD沿AD翻折，使O点落在AB边上的E点处，得到∠OAD=∠EAD=45°，DE=OD，求出OD=2，得出D点的坐标，再根据DE=OD=2，求出E点的坐标；
（2）由翻折可知四边形AODE为正方形，过M作MH⊥BC于H，先求出∠NMH=∠MNH=45°，得出NH=MH，求出MN的长，再根据直线OE的解析式，依题意得MN∥OE，设MN的解析式为y=x+b，确定出直线DE的解析式与直线BC的解析式，进而表示出M与N坐标，表示出CM，CN，MN，分三种情况考虑：①当CM=CN时；②当CM=MN时；③当CM=MN时，分别求出满足题意M的坐标即可．

解答 解：（1）∵将△AOD沿AD翻折，使O点落在AB边上的E点处，
∴∠OAD=∠EAD=45°，DE=OD，
∴OA=OD，
∵OA=2，
∴OD=2，
∴D点坐标是（2，0），DE=OD=2，
∴E点坐标是（2，2），
故答案为：（2，0），（2，2）；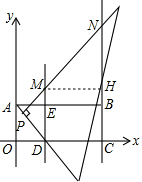

（2）存在点M使△CMN为等腰三角形，理由如下：
由翻折可知四边形AODE为正方形，
过M作MH⊥BC于H，如图所示，
∵∠PDM=∠PMD=45°，则∠NMH=∠MNH=45°，
NH=MH=4，MN=4$\sqrt{2}$，
∵直线OE的解析式为：y=x，依题意得MN∥OE，
∴设MN的解析式为y=x+b，
而DE的解析式为x=2，BC的解析式为x=6，
∴M（2，2+b），N（6，6+b），
∴CM=$\sqrt{{4}^{2}+（2+b）^{2}}$，CN=6+b，MN=4$\sqrt{2}$，
分三种情况讨论：
①当CM=CN时，根据勾股定理得：4²+（2+b）²=（6+b）²，
解得：b=-2，此时M（2，0）；
②当CM=MN时，根据勾股定理得：4²+（2+b）²=（4$\sqrt{2}$）²，
解得：b₁=2，b₂=-6（不合题意舍去），此时M（2，4）；
③当CN=MN时，6+b=4$\sqrt{2}$，
解得：b=4$\sqrt{2}$-6，此时M（2，4$\sqrt{2}$-4）；
综上所述，存在点M使△CMN为等腰三角形，M点的坐标为：（2，0），（2，4），（2，4$\sqrt{2}$-4）．

点评 此题属于一次函数综合题，涉及的知识有：折叠的性质，坐标与图形性质，勾股定理，等腰直角三角形的判定与性质，以及待定系数法确定一次函数解析式，熟练掌握一次函数性质是解本题的关键．