题目内容
9.已知abc≠0,且$\frac{a}{b}=\frac{b}{c}=\frac{c}{a}$,求$\frac{3a+2b+c}{a-2b-3c}$的值.分析 分类讨论:当a+b+c=0时,根据△,可得方程无解;当a+b+c≠0,根据等比性质,可得答案.
解答 解:当a+b+c=0时,即b=-a-c,
由$\frac{a}{b}=\frac{b}{c}=\frac{c}{a}$,得
c2=-a2-ac,
($\frac{a}{c}$)2+$\frac{a}{c}$+1=0,
△=1-4<0,
a,c无解;
(2)当a+b+c≠0时,有等比性质,得
$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{a}$=$\frac{a+b+c}{b+c+a}$=1,
a=b=c.
$\frac{3a+2b+c}{a-2b-3c}$=$\frac{3a+2a+a}{a-2a-3a}$=-$\frac{3}{2}$.
点评 本题考查了比例的性质,分类讨论,以防遗漏,利用了等比性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列为真命题的是( )
| A. | 相等的角是对顶角 | B. | 直角三角形都相似 | ||
| C. | 两直线平行,同旁内角相等 | D. | 两点之间线段最短 |
 已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),
已知(如图所示)A(3,2),B(3,4),C(-4,-2),D(2,-2),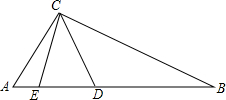 马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由.
马明和王群在解这样一道题:“如图,在△ABC中,∠ACB=90°,点D、E在边AB上,AD=AC,BE=BC.求∠DCE的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B有关,只有告诉∠B的度数才能求出∠DCE的度数.”王群说:“∠DCE的度数是一个定值,与∠B的度数无关.”他们谁说的正确?请说明理由.