题目内容
 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
(1)求证:CD是半⊙O的切线;
(2)若OA=2,求AC的长.
 (1)证明:连接OC.
(1)证明:连接OC.∵OA=OC,∠A=30°,
∴∠A=∠ACO=30°,
∴∠COD=60°.
又∵AC=CD,
∴∠A=∠D=30度.
∴∠OCD=180°-60°-30°=90°,
∴CD是半⊙O的切线.
(2)解:连接BC.
∵AB是直径,
∴∠ACB=90°.
在Rt△ABC中,∵cosA=
 ,
,∴AC=ABcos30°=4×
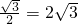 ,
,∴AC=
 .
.分析:要证明CD是半⊙O的切线只要证明∠OCD=90°即可;
根据三角函数即可求得AC的长.
点评:此题考查学生对切线的判定及解直角三角形的综合运用.

练习册系列答案
相关题目
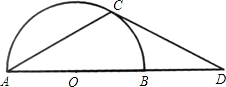 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.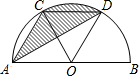 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.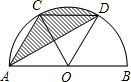 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为 (2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( )
(2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( ) 如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为
如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为