题目内容
如图，在Rt△ABC中，∠C=90°，CD⊥AB，垂足为D，AD=2，DB=8，则CD的长为考点：相似三角形的判定与性质,射影定理
专题：
分析：根据直角三角形的性质可以证明△ACD∽△CBD，然后根据相似三角形的对应边的比相等即可求解．
解答：解：∵在Rt△ABC中，∠C=90°，CD⊥AB，垂足为D，
∴△ACD∽△CBD，
∴
=
，即
=
，
解得：CD=4．
故答案是：4．
∴△ACD∽△CBD，
∴
| AD |
| CD |
| CD |
| DB |
| 2 |
| CD |
| CD |
| 8 |
解得：CD=4．
故答案是：4．
点评：本题考查了相似三角形的判定与性质，理解△ACD∽△CBD是关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
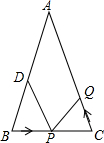如图，在△ABC中，AB=AC=10厘米，∠B=∠C，BC=8厘米，点D为AB的中点，如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动，当一个点停止运动时，另一个点也随之停止运动，当点Q的运动速度为
如图，△ABC的周长为28cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连接AD．若AE=4cm，则△ABD的周长是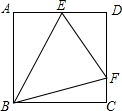
如图，在正方形ABCD中，点E是AD边的中点，F是CD边上一点，且∠EBF=45°，则tan∠EFB的值为
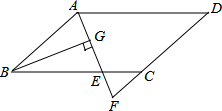如图，在?ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G．若BG=4