题目内容
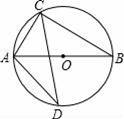
如图,AB是⊙O的弦,AB=6,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是 .


3
 .
.

【考点】三角形中位线定理;等腰直角三角形;圆周角定理.
【专题】压轴题.
【分析】根据中位线定理得到MN的最大时,AC最大,当AC最大时是直径,从而求得直径后就可以求得最大值.
【解答】解:∵点M,N分别是AB,BC的中点,
∴MN=
 AC,
AC,
∴当AC取得最大值时,MN就取得最大值,
当AC时直径时,最大,
如图,


∵∠ACB=∠D=45°,AB=6,
∴AD=6
 ,
,
∴MN=
 AD=3
AD=3

故答案为:3
 .
.
【点评】本题考查了三角形的中位线定理、等腰直角三角形的性质及圆周角定理,解题的关键是了解当什么时候MN的值最大,难度不大.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
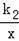
 (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.