题目内容
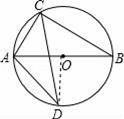
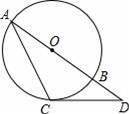
如图,⊙O的直径为8cm,∠B=30°,∠ACB的平分线交⊙O于D,连接AD.
(1)求BC的长;
(2)求∠CAD的度数.
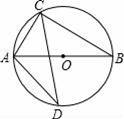

【考点】圆周角定理.
【分析】(1)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,又由⊙O的直径为8cm,∠B=30°,即可求得答案;
(2)首先连接OD,由CD是∠ACB的角平分线,可求得∠BAD的度数,继而求得答案.
【解答】解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=8cm,∠B=30°,
∴AC=
 AB=4cm,
AB=4cm,
∴BC=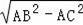
 =4
=4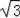
 cm;
cm;
(2)连接OD,
∵CD是∠ACB的角平分线,
∴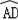
 =
=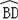
 ,
,
∴∠BOD=
 ∠AOB=90°,
∠AOB=90°,
∴∠BAD=
 ∠BOD=45°,
∠BOD=45°,
∵∠BAC=90°﹣∠B=60°,
∴∠CAD=∠BAC+∠BAD=105°.

【点评】此题考查了圆周角定理以及含30°角的直角三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ;
;

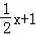
 的图象与x轴交于A点,与y轴交于B点:抛物线y=
的图象与x轴交于A点,与y轴交于B点:抛物线y=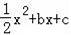
 的图象余一次函数y=
的图象余一次函数y=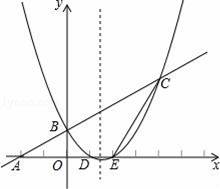


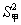 =79.6,
=79.6,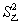 =68.5.由此可知
=68.5.由此可知 :在该地区____种水稻更具有推广价值.
:在该地区____种水稻更具有推广价值.