题目内容
设
=
=
=k,则直线y=k(x+1)一定经过( )
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
分析:由于a+b+c的值不能确定,故应分两种情况进行讨论,当a+b+c≠0时可得出k=
,由一次函数的性质可判断出直线为y=
x+
所经过的象限;当a+b+c=0时,即a+b=-c,则k=-1,此时直线为y=-x-1,由一次函数的性质可判断出直线经过的象限,故可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:分情况讨论:
当a+b+c≠0时,根据比例的等比性质,得:k=
=
,此时直线为y=
x+
,直线一定经过一、二、三象限;
当a+b+c=0时,即a+b=-c,则k=-1,此时直线为y=-x-1,即直线必过二、三、四象限.
故直线必过第二、三象限.
故选B.
当a+b+c≠0时,根据比例的等比性质,得:k=
| a+b+c |
| 2(a+b+c) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当a+b+c=0时,即a+b=-c,则k=-1,此时直线为y=-x-1,即直线必过二、三、四象限.
故直线必过第二、三象限.
故选B.
点评:本题考查的是一次函数的图象与系数的关系,解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 23、如图,已知正方形ABCD,设AB、BC的延长线分别为射线BK,CN,点F从A点沿射线AB以一定的速度运动,同时点E从B点沿射线BC以相同的速度运动,FD交AE于点M.
23、如图,已知正方形ABCD,设AB、BC的延长线分别为射线BK,CN,点F从A点沿射线AB以一定的速度运动,同时点E从B点沿射线BC以相同的速度运动,FD交AE于点M.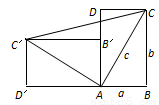
 ,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
 +
+ )π
)π +
+ )π
)π π
π