Question

6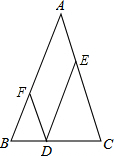．如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DE∥BA，DF∥CA．
（1）求证：∠EDF=∠A；
（2）试判断：∠A+∠B+∠C等于多少度？并说明理由．

Answer 1

分析 （1）根据平行线的性质证明即可；
（2）先根据平行线的性质得出∠A=∠FDE，再由平角的定义即可得出结论．

解答 （1）证明：∵DE∥BA，
∴∠FDE=∠BFD；
∵DF∥CA，
∴∠A=∠BFD，
∴∠FDE=∠A；
（2）∠A+∠B+∠C=180°，
理由：证明：∵DE∥BA
∴∠FDE=∠BFD（两直线平行，内错角相等），
∴∠B=∠EDC（两直线平行，同位角相等）．
∵DF∥CA，
∴∠A=∠BFD，∠C=∠BDF（两直线平行，同位角相等），
∴∠A=∠FDE．
∵∠FDE+∠CDE+∠BDF=180°（平角的定义），
∴∠A+∠B+∠C=180°（等量代换）．

点评 本题考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键．