Question

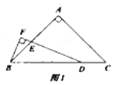
【题目】如图，在正方形中，点是对角线的中点，是线段上的动点（不与点，重合），交于点，于点．则对于下列结论：①；②；③；④，其中错误结论的个数是（ ）

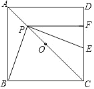
A.0B.1C.2D.3

Answer 1

【答案】B

【解析】

连接PD，证明△PBC≌△PDC得出∠PBC=∠PDE，PB=PD，证出∠PDE=∠PED，得出PD=PE，因此PE=PB，①正确；由等腰三角形的性质得出DF=EF，②正确；

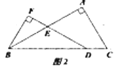
作PH⊥AD于点H，则得出，即，得出，③正确；证出PF∥AD，得出，由DF≠CE得出，④错误；即可得出结论．

连接PD，如图1所示：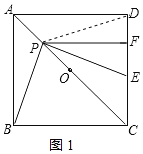

∵四边形ABCD是正方形，

∴BC=DC，∠BCP=∠DCP，

在△PBC和△PDC中，，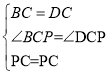

∴△PBC≌△PDC（SAS）

∴∠PBC=∠PDE，PB=PD，

∵PB⊥PE，∠BCD=90°，

∴∠PBC+∠PEC=360°-∠BPE-∠BCE=180°

∵∠PEC+∠PED=180°，

∴∠PBC=∠PED，

∴∠PDE=∠PED，

∴PD=PE，

∴PE=PB，①正确；

∵PD=PE，PF⊥CD，

∴DF=EF，②正确；

作PH⊥AD于点H，如图2所示：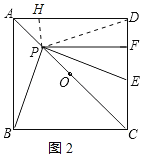

则

∴，即，

∴，③正确；

∵PF⊥CD，AD⊥CD，
∴PF∥AD，

∴，

∵DF≠CE，

∴，④错误；

错误结论的个数有1个；
故答案为：B．