Question

【题目】已知，△ABC中，AB＝AC，点F在边BC上

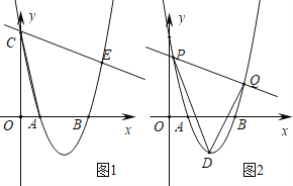
（1）如图1，AF＝BF，求证：AB2＝BFBC；

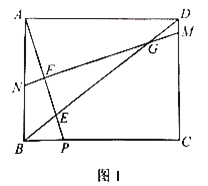
（2）如图2，FC＝2BF，点E、M在直线AB上，EF∥AC，cosB＝n，且FM2＝MEMB

①若M在边AB上，求的值（用含n的式子表示）；

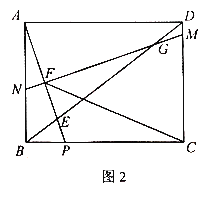
②若M在BA的延长线上时，直接写出n的范围．

Answer 1

【答案】（1）见解析；（2）①8n2﹣3；②＜n＜

【解析】

（1）只要证明△BAF∽△BCA即可解决问题．

（2）①如图2中，作AD⊥BC于D，延长FM交CA的延长线于G．设DF＝m．想办法求出AC，EF，CG（用m，n表示）即可解决问题．

②如图3中，求出当点M与A重合时n的，由题意∠B＜60°，故n＞，由此即可判断．

（1）证明：如图1中，

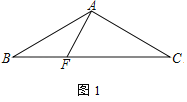
∵AB＝AC，FB＝FA，

∴∠B＝∠C＝∠BAF，

∵∠B＝∠B，∠BAF＝∠C，

∴△BAF∽△BCA，

∴＝，

∴AB2＝BFBC．

（2）①解：如图2中，作AD⊥BC于D，延长FM交CA的延长线于G．设DF＝m．

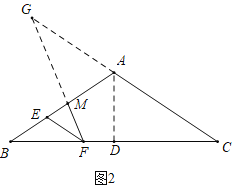
∵AB＝AC，AD⊥BC，

∴BD＝DC，

∵FC＝2BF，DF＝m，

∴BF＝2m，FC＝4m，BD＝3m，

∵cosB＝n＝，

∴AB＝AC＝，

∵EF∥AC，

∴＝＝，

∴EF＝，

∵FM2＝MEMB，

∴＝，

∵∠FME＝∠FMB，

∴△FME∽△BMF，

∴∠MFE＝∠B，

∵EF∥CG，

∴∠G＝∠MFE＝∠B＝∠C，

∴FC＝FG＝4m，

∵△EFB∽△FCG，

∴＝，

∴＝，

∴CG＝8mn，

∵EF∥AG，

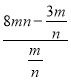∴＝＝＝8n2﹣3．

②解：如图3中，当点M与A重合时，

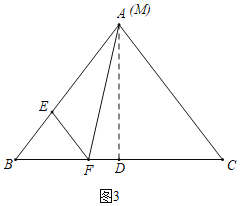
由①可知：8mn＝，解得n＝（负根已经舍弃），

由题意∠B＜60°，故n＞

观察图象可知M在BA的延长线上时，＜n＜．