题目内容
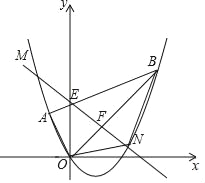
【题目】如图,已知抛物线![]() 与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
与x轴交于A(1,0),B(3,0)两点与y轴交于点C,D为抛物线顶点.
(1)求抛物线的解析式;
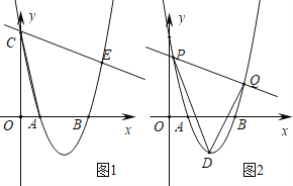
(2)如图1,过点C的直线交抛物线于另一点E,若∠ACE=60°,求点E的坐标.
(3)如图2,直线![]() 交抛物线于P,Q两点,求△DPQ面积的最小值.
交抛物线于P,Q两点,求△DPQ面积的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)△DPQ面积的最小值为
;(3)△DPQ面积的最小值为![]()
【解析】
(1)由抛物线与x轴的两个交点坐标A(1,0),B(3,0),可代入点的坐标即可得解;
(2)过点A作AF⊥AC交AC的延长线于点F,过点F作FG⊥x轴交x轴于点G,可证明△AOC∽△FGA,利用60°角的锐角三角函数值和比例线段可求出AG和FG的长,则F点坐标为(10,![]() ),求得直线CF的解析式,与抛物线方程联立即求出点E的坐标;
),求得直线CF的解析式,与抛物线方程联立即求出点E的坐标;
(3)过点D作DM∥y轴交PQ于点M,由抛物线顶点D的坐标可知DM=2![]() ,若△DPQ面积有最小值,则底边是定值,点P和点Q的横坐标之差的绝对值最小.联立直线与抛物线方程可用k表示出点P和点Q的横坐标之差的绝对值,即可得解.
,若△DPQ面积有最小值,则底边是定值,点P和点Q的横坐标之差的绝对值最小.联立直线与抛物线方程可用k表示出点P和点Q的横坐标之差的绝对值,即可得解.
解:(1)∵抛物线y=ax2+bx+3![]() 与x轴交于A(1,0),B(3,0)两点
与x轴交于A(1,0),B(3,0)两点
∴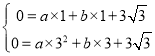
解得:a=![]() ,b=
,b=![]() ;
;
∴所求抛物线的解析式为:![]() ;
;
(2)如图1所示,过点A作AF⊥AC交CE的延长线于点F,过点F作FG⊥x轴交x轴于点G,
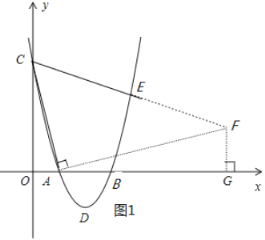
∵∠COA=∠CAF=∠FGA=90°,
∴∠OCA=∠GAF,∠OAC=∠GFA
∴△AOC∽△FGA,
∴![]()
又∵△CAF是直角三角形,∠ACE=60°
∴![]() ,
,
∴![]() ,
,
∵OC=3![]() ,OA=1,
,OA=1,
∴FG=![]() ,AG=9,
,AG=9,
∴F![]() ,
,
设直线CF的解析式为:y=mx+n,
将![]() 分别代入上式,
分别代入上式,
得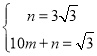 ,
,
解得: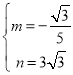 ,
,
∴直线CF的解析式为:![]() ,
,
联立直线CF与抛物线的解析式得
∴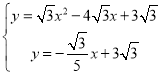 ,
,
解得: (不符合题意),
(不符合题意),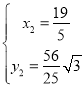 ,
,
∴所求点E的坐标为:![]() ;
;
(3)如图2,过点D作DM∥y轴交PQ于点M,
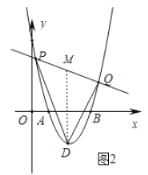
∵![]() =
=![]()
∴![]() ,
,
把x=2代入直线y=kx-2k+![]() 得y=
得y=![]() ,
,
∴DM=![]() ,
,
∵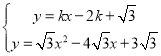 ,
,
整理得![]() ,
,
∴P、Q两点的横坐标x1、x2为方程![]() 的两根,
的两根,
∴![]() =
=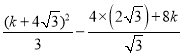 =
=![]() ,
,
当k=0时,![]() 的最小值为8,此时|x1-x2|的最小值为2
的最小值为8,此时|x1-x2|的最小值为2![]() .
.
∵![]() =
=![]() |x1-x2|.
|x1-x2|.
∴△DPQ面积的最小值为:![]() .
.