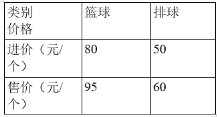
题目内容
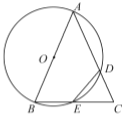
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() .
.![]() 为弧
为弧![]() 中点,过点
中点,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OC.由点C为![]() 的中点,得到
的中点,得到![]() ,求得∠COB=∠COF,根据平行线的性质得到∠OCG=∠OMB=90°,于是得到CG是⊙O的切线;
,求得∠COB=∠COF,根据平行线的性质得到∠OCG=∠OMB=90°,于是得到CG是⊙O的切线;
(2)连接BC.由(1)知,∠COB=∠COF=![]() ∠BOF=60°,推出△OBC为等边三角形.得到∠OCD=30°,则EM=
∠BOF=60°,推出△OBC为等边三角形.得到∠OCD=30°,则EM=![]() CE=2,根据勾股定理得到CM=
CE=2,根据勾股定理得到CM=![]() ,求得OM=CM=
,求得OM=CM=![]() ,于是得到结论.
,于是得到结论.
(1)证明:连接OC.
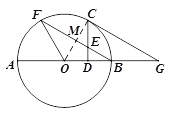
.∵点C为![]() 的中点,
的中点,
∴![]() ,
,
∴∠COB=∠COF,
∵OB=OF,
∴OC⊥BF,
设垂足为M,则∠OMB=90°,
∵CG∥FB,
∴∠OCG=∠OMB=90°,
∴CG是⊙O的切线;
(2)连接BC.
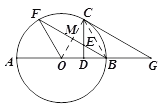
由(1)知,∠COB=∠COF=![]() ∠BOF=60°,
∠BOF=60°,
∵OB=OC,
∴△OBC为等边三角形.
∴∠OCD=30°,则EM=![]() CE=2,
CE=2,
∴CM=![]() .
.
根据等腰三角形“三线合一”得OM=CM=![]() ,
,
∴OC=4![]() ,
,
即⊙O的半径为4![]() .
.

练习册系列答案
相关题目