Question

【题目】在平面直角坐标系中，抛物线的顶点为，且经过点，与轴分别交于、两点.

（1）求直线和抛物线的函数表达式；

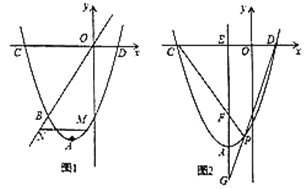
（2）如图，点是抛物线上的一个动点，且在直线的下方，过点作轴的平行线与直线交于点，求的最大值；

（3）如图，过点的直线交轴于点，且轴，点是抛物线上、之间的一个动点，直线、与分别交于、两点.当点运动时，是否为定值？若是，试求出该定值；若不是，请说明理由.

Answer 1

【答案】（1），；（2）；（3）为定值8，见解析.

【解析】

（1）设直线解析式为，把代入求解即可；设抛物线解析式为，代入求解即可；

（2）设，，则的横坐标为，纵坐标为，表示出的长，利用二次函数的性质求解即可；

（3）过点作轴交轴于，先求出点C和点D的坐标，设，则，，，根据，表示出EF的长，根据表示出EG的长，然后表示出，整理即可求出结论.

解：（1）设直线解析式为，由题意可得，解得，

∴直线解析式为，

∵抛物线顶点坐标为，∴可设抛物线解析式为，

∵抛物线经过，∴，解得，

∴抛物线为；

（2）设，，则的横坐标为，纵坐标为，

∵轴，∴，得，

∴当时，有最大值，最大值为；

（3）.

理由如下：如图2，过点作轴交轴于，

在中，令可得，解得或，

∴，，

设，则，，，

∵，∴，

∴，∴，

同理得，

∴，

∴

，

∴当点运动时，为定值8.