题目内容
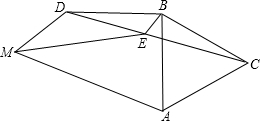 如图,在四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,BE平分∠ABD交CD于E,连ME,若BD=
如图,在四边形ABDM中,AB=BD,AB⊥BD,∠AMD=60°,以AB为边作等边△ABC,BE平分∠ABD交CD于E,连ME,若BD=| 6 |
考点:全等三角形的判定与性质
专题:
分析:易求得∠DBC=150°,BD=BC,即可求得∠BDE度数,再根据BE平分∠ABD可求得∠BDE度数,即可求得DE的长度,再根据BD,BC可求得CD的长,即可解题.
解答:解:连接AD,延长BE交AD于点H,

∵AB=BD=BC,∠ABD=90°,∠ABC=60°,
∴∠BDC=∠BCD=15°,
∵AB=BD=
,BE平分∠ABD,AB⊥BD,
∴DH=AH=BH=
AD=
×
BD=
,∠BDH=45°,BH⊥AD,
∴∠EDH=∠BDH-∠BDE=30°,
在RT△DEH中,∠EDH=30°,DH=
,
∴DE=
=2,
∵CD=
=
=3+
,
∴CE=CD-DE=3+
-2=
+1.

∵AB=BD=BC,∠ABD=90°,∠ABC=60°,
∴∠BDC=∠BCD=15°,
∵AB=BD=
| 6 |
∴DH=AH=BH=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
∴∠EDH=∠BDH-∠BDE=30°,
在RT△DEH中,∠EDH=30°,DH=
| 3 |
∴DE=
| DH |
| cos30° |
∵CD=
| BD2+BC2-2BD•BC•cos150° |
6+6-2
|
| 3 |
∴CE=CD-DE=3+
| 3 |
| 3 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求得DE的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把10-(+4)+(-6)-(-5)写成省略括的和是( )
| A、10-4-6-5 |
| B、10-4-6+5 |
| C、10+(-4)+(-6)+5 |
| D、10+4-6-5 |
2011年我国的“天宫一号”发射升空,在轨道上运行时,它将保持每小时28440公里的速度,此速度有第一宇宙速度之称.这个速度用科学记数法(保留3个有效数字)表示为( )
| A、28.4×104公里 |
| B、2.84×106公里 |
| C、2.84×105公里 |
| D、2.84×l04公里 |