题目内容
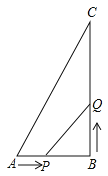
【题目】如图,在直角三角形![]() 中,
中,![]() ,点
,点![]() 从
从![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.
的速度移动. ![]() 分别从
分别从![]() 同时出发,当一个动点到达终点则另一动点也随之停止运动,
同时出发,当一个动点到达终点则另一动点也随之停止运动,
(1)求![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(2)是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(3)点![]() 在运动的过程中,是否存在某时刻
在运动的过程中,是否存在某时刻![]() , 直线
, 直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分?若存在,求出
两部分?若存在,求出![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
【答案】(1)2;(2)存在,![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)根据题意用t表示出BP、BQ,根据等腰三角形的概念列方程,解方程得到答案;
(2)根据线段垂直平分线的性质得到QA=QC,列方程,解方程即可;
(3)分AC+AP+CQ=2(BP+BQ)、2(AC+AP+CQ)=BP+BQ两种情况计算,得到答案.
![]() 由题意得,
由题意得,![]()
则![]()
当![]() 为等腰三角形时,
为等腰三角形时,
只有![]()
![]()
解得,![]()
![]() 当点
当点![]() 在线段
在线段![]() 的垂直平分线上时,连接QA,
的垂直平分线上时,连接QA,

![]()
设![]()
则![]()
解得,![]() 即
即![]()
![]() (秒)
(秒)
![]() 在
在![]() 中,
中,
![]()
当直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分时,
两部分时,
①当![]() 时,
时,
![]()
解得,![]()
②当![]() 时,
时,
![]()
解得,![]()
![]() 当
当![]() 或
或![]() 时,直线
时,直线![]() 把
把![]() 的周长分为
的周长分为![]() 两部分.
两部分.

练习册系列答案
相关题目