��Ŀ����
����Ŀ����������ɳˮ����ʳ�������.��һ��ΰ��ë�ļѾ䣬���������������������.ij����ר������ij��Ʒ����հ�װ���������ʳ��Ʒ���ɱ�Ϊ30Ԫ/�У�ÿ������y(��)�����۵���x(Ԫ)֮�����һ�κ�����ϵ����ͼ��ʾ��
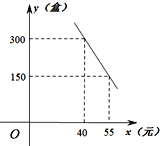
(1)��y��x֮��ĺ�����ϵʽ��
(2)����涨ÿ�������������ʳ��Ʒ��������������240�У������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
(3)������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3 600Ԫ����ȷ�������������ʳ��Ʒ���۵��۵ķ�Χ��
���𰸡�(1)y����10x��700��(2)���۵���Ϊ46Ԫʱ��ÿ���ȡ������������������3840Ԫ��(3)45��x��55ʱ������ÿ��ʣ��������3600Ԫ��
��������
��1�����ô���ϵ������ȷ��y��x֮��ĺ�����ϵʽ��
��2����������=������������������Ȼ��1���еĺ���ʽ�������У������������۵���֮��Ĺ�ϵʽ��Ȼ��������������жϳ��������
��3�����ȵó�w��x�ĺ�����ϵʽ���������������������3600Ԫʱ����Ӧx��ֵ�����������ԣ����x��ȡֵ��Χ��
(1)��y��x�Ĺ�ϵʽ��![]() ���������
���������
![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy����10x��700
(2)�����⣬�ã�10x��700��240�����x��46��
������ΪW��(x��30)y��(x��30)(��10x��700)
����10x2��1 000x��21 000����10(x��50)2��4 000��
�ߣ�10��0��
��x��50ʱ��W��x�����������
��x��46ʱ��W���ֵ����10(46��50)2��4000��3840��
�𣺵����۵���Ϊ46Ԫʱ��ÿ���ȡ������������������3840Ԫ��
(3)W��150����10x2��1 000x��21000��150��3600��
��10(x��50)2����250��
x��50����5��
x1��55��x2��45��
��ͼ��ʾ����ͼ��ã�

��45��x��55ʱ������ÿ��ʣ��������3600Ԫ��

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�