题目内容
12.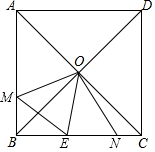 如图,正方形ABCD的两条对角线AC、BD相交于点O,点M、N分别为AB、BC边上的点,且∠MON=90°,由OE平分∠MON交BC边于点E,连接ME.则下列结论:
如图,正方形ABCD的两条对角线AC、BD相交于点O,点M、N分别为AB、BC边上的点,且∠MON=90°,由OE平分∠MON交BC边于点E,连接ME.则下列结论:①△BOM≌△CON;②ME=EN;③BE2+CN2=ON2;④EO2=EN•EC.
其中正确的结论是①②④(填写所有正确结论的序号)
分析 ①正确.根据ASA即可证明;
②正确.只要证明△EOM≌△EON,可得EM=EN;
③错误.易证BE2+CN2=EM2,显然EM≠ON,故③错误;
④正确.只要证明△OEN∽△CEO,可得$\frac{OE}{CE}$=$\frac{EN}{OE}$,由此即可证明;
解答 解:∵四边形ABCD是正方形,
∴OB=OC,∠OBM=∠OCN=45°,AC⊥BD,
∴∠MON=∠BOC=90°,
∴∠BOM=∠CON,
在△BOM和△CON中,
$\left\{\begin{array}{l}{∠BOM=∠CON}\\{OB=OC}\\{∠OBM=∠OCN}\end{array}\right.$,
∴△BOM≌△CON,故①正确,
∴OM=ON,BM=CN,
∵∠EON=∠EOM=45°,EO=EO,
∴△EOM≌△EON,
∴EM=EN,故②正确,
在Rt△EMB中,BE2+BM2=EM2,
∴BE2+CN2=EM2,显然EM≠ON,故③错误,
∵∠EON=∠ECO,∠OEN=∠OEC,
∴△OEN∽△CEO,
∴$\frac{OE}{CE}$=$\frac{EN}{OE}$,
∴OE2=EN•EC,故④正确.
故答案为①②④
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质、正方形的性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
3. 如图,数轴上表示的关于x的一元一次不等式组的解集为( )
如图,数轴上表示的关于x的一元一次不等式组的解集为( )
 如图,数轴上表示的关于x的一元一次不等式组的解集为( )
如图,数轴上表示的关于x的一元一次不等式组的解集为( )| A. | x≥3 | B. | x>3 | C. | 3>x>-1 | D. | -1<x≤3 |
17.某种细菌用肉眼是根本看不到的,用显微镜测其直径大约是0.000005米,将0.000005用科学记数法表示为( )
| A. | 50×10-7 | B. | 50×10-5 | C. | 50×10-3 | D. | 5×10-6 |
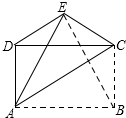 如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=$\sqrt{3}$,则CD的长为2$\sqrt{3}$.
如图,将矩形ABCD沿直线AC折叠,点B落在点E处,连接DE,BE,若△ABE为等边三角形,且S△CDE=$\sqrt{3}$,则CD的长为2$\sqrt{3}$.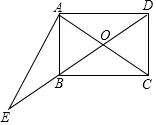 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.