题目内容
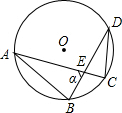 如图⊙O的半径为1cm,弦AB、CD的长度分别为
如图⊙O的半径为1cm,弦AB、CD的长度分别为| 2 |
分析:根据勾股定理的逆定理可证△AOB是等腰直角三角形,故可求∠OAB=∠OBA=45°,又由已知可证△COD是等边三角形,所以∠ODC=∠OCD=60°,根据圆周角的性质可证∠CDB=∠CAB,而∠ODB=∠OBD,所以∠CAB+∠OBD=∠CDB+∠ODB=∠ODC=60°,再根据三角形的内角和定理可求α.
解答: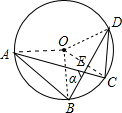 解:连接OA、OB、OC、OD,
解:连接OA、OB、OC、OD,
∵OA=OB=OC=OD=1,AB=
,CD=1,
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°-∠CAB-∠OBA-∠OBD=180°-∠OBA-(∠CDB+∠ODB)=180°-45°-60°=75°.
故选:A.
 解:连接OA、OB、OC、OD,
解:连接OA、OB、OC、OD,∵OA=OB=OC=OD=1,AB=
| 2 |
∴OA2+OB2=AB2,
∴△AOB是等腰直角三角形,
△COD是等边三角形,
∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,
∵∠CDB=∠CAB,∠ODB=∠OBD,
∴α=180°-∠CAB-∠OBA-∠OBD=180°-∠OBA-(∠CDB+∠ODB)=180°-45°-60°=75°.
故选:A.
点评:本题考查了勾股定理的逆定理,圆周角的性质,等边三角形的性质以及三角形的内角和定理.

练习册系列答案
相关题目
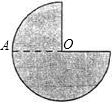 如图,把半径为1的四分之三圆形纸片沿半径OA剪开,依次用得到的半圆形纸片和四分之一圆形纸片做成两个圆锥的侧面,则这两个圆锥的底面积之比为( )
如图,把半径为1的四分之三圆形纸片沿半径OA剪开,依次用得到的半圆形纸片和四分之一圆形纸片做成两个圆锥的侧面,则这两个圆锥的底面积之比为( )| A、5:1 | B、4:1 | C、3:1 | D、2:1 |
 如图,将半径为2的圆形纸片,沿半径OA、OB将其裁成1:3两个部分,用所得扇形围成圆锥的侧面,则圆锥的底面半径为( )
如图,将半径为2的圆形纸片,沿半径OA、OB将其裁成1:3两个部分,用所得扇形围成圆锥的侧面,则圆锥的底面半径为( )A、
| ||||
| B、1 | ||||
| C、1或3 | ||||
D、
|
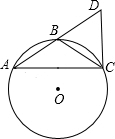 如图,在半径为3的⊙O中,B是劣弧AC的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD等于( )
如图,在半径为3的⊙O中,B是劣弧AC的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD等于( ) 如图,在半径为
如图,在半径为