题目内容
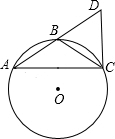如图，在半径为3的⊙O中，B是劣弧AC的中点，连接AB并延长到D，使BD=AB，连接AC、BC、CD，如果AB=2，那么CD等于（ ）| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
分析：如图，连OA，OB．利用垂径定理和勾股定理求BE，利用中位线定理求CD．
解答：
解：如图，连OA，OB，
∵B是弧AC的中点，AB=BC=BD，
∴△ACD是直角三角形，∠ACD=90°，
由垂径定理知，OB⊥AC，点E是AC的中点，
由勾股定理知，OA2=AE2+OE2，AE2+BE2=AB2，
∵AB=2，AO=BO=3，代入解得，BE=
，
∵∠AEB=∠ACD=90°，
∴BE∥CD，
∵点B是AD的中点，所以BE是△ACD的中位线，所以CD=2BE=
．
故选D．
解：如图，连OA，OB，∵B是弧AC的中点，AB=BC=BD，
∴△ACD是直角三角形，∠ACD=90°，
由垂径定理知，OB⊥AC，点E是AC的中点，
由勾股定理知，OA2=AE2+OE2，AE2+BE2=AB2，
∵AB=2，AO=BO=3，代入解得，BE=
| 2 |
| 3 |
∵∠AEB=∠ACD=90°，
∴BE∥CD，
∵点B是AD的中点，所以BE是△ACD的中位线，所以CD=2BE=
| 4 |
| 3 |
故选D．
点评：本题考查了垂径定理、勾股定理以及直角三角形的判定和性质．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
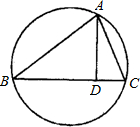如图，在半径为R的圆中作一内接△ABC，使BC边上的高AD=h（定值），这样的三角形可作出无数个，但AB•AC为定值，其值为
如图，在半径为R的圆内作一个内接正方形，然后作这个正方形的内切圆，又在这个内切圆中作内接正方形，依此作到第n个内切圆，它的半径是（ ）A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
如图，在半径为2的⊙O中，弦AB的长为2
（2012•陕西）如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（ ）
（2013•上海模拟）如图，在半径为1的扇形AOB中，∠AOB=90°，点P是