题目内容
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1) (1)A(2,0);C(0,4);(2) 直线CD解析式为y=-![]() x+4.(3)P1(0,0);P2(
x+4.(3)P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).
【解析】
试题分析:(1)已知直线y=-2x+4与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(3)将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
试题解析:(1)A(2,0);C(0,4)
(2)由折叠知:CD=AD.设AD=x,则CD=x,BD=4-x,
根据题意得:(4-x)2+22=x2解得:x=![]()
此时,AD=![]() ,D(2,
,D(2,![]() )
)
设直线CD为y=kx+4,把D(2,![]() )代入得
)代入得![]() =2k+4
=2k+4
解得:k=-![]()
∴该直线CD解析式为y=-![]() x+4.
x+4.
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图,
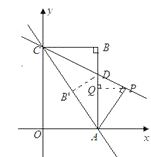
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=![]() ,PD=BD=4-
,PD=BD=4-![]() =
=![]() ,AP=BC=2
,AP=BC=2
由AD×PQ=DP×AP得:![]() PQ=3
PQ=3
∴PQ=![]()
∴xP=2+![]() =
=![]() ,
,
把x=![]() 代入y=-
代入y=-![]() x+4得y=
x+4得y=![]()
此时P(![]() ,
,![]() )
)
(也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标)
③当点P在第二象限时,如图
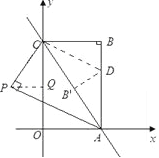
同理可求得:CQ=![]()
∴OQ=4-![]() =
=![]()
此时P(-![]() ,
,![]() )
)
综合得,满足条件的点P有三个,
分别为:P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).

 优学名师名题系列答案
优学名师名题系列答案【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差( | |
初中部 | a | 85 | b |
|
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差![]() ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.